广东2018-2019学年中考数学模拟冲刺考试试卷
试卷更新日期:2019-06-28 类型:中考模拟
一、选择题(本大题10小题,每小题3分,共30分)
-
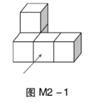
1. 2的倒数是( )A、 B、-2 C、 D、22. 由若干个相同的正方体组成的几何体如图M2-1,则这个几何体的俯视图是( )
 A、
A、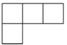 B、
B、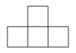 C、
C、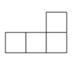 D、
D、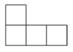 3. 下列计算正确的是( )A、b3·b3=2b3 B、(-2a)2=4a2 C、(a+b)2=a2+b2 D、(x+2)(x-2)=x2-24. 已知∠A=70°,则∠A的余角等于( )A、20° B、30° C、70° D、110°5. 如图M2-2,A,B两点被一座山隔开,M,N分别是AC,BC的中点,测量MN的长度为40m,那么AB的长度为( )
3. 下列计算正确的是( )A、b3·b3=2b3 B、(-2a)2=4a2 C、(a+b)2=a2+b2 D、(x+2)(x-2)=x2-24. 已知∠A=70°,则∠A的余角等于( )A、20° B、30° C、70° D、110°5. 如图M2-2,A,B两点被一座山隔开,M,N分别是AC,BC的中点,测量MN的长度为40m,那么AB的长度为( )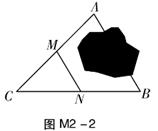 A、40m B、80m C、160m D、不能确定6. 如果△ABC∽△DEF,且相似比为2:3,则它们对应边上的高之比为( )A、2:3 B、4:9 C、3:5 D、9:47. 方程4x2-2x+ =0根的情况是( )A、有两个相等的实数根 B、方程根的情况不能确定 C、没有实数根 D、有两个不相等的实数根8. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、40m B、80m C、160m D、不能确定6. 如果△ABC∽△DEF,且相似比为2:3,则它们对应边上的高之比为( )A、2:3 B、4:9 C、3:5 D、9:47. 方程4x2-2x+ =0根的情况是( )A、有两个相等的实数根 B、方程根的情况不能确定 C、没有实数根 D、有两个不相等的实数根8. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD9. 一个扇形的弧长为4π,半径长为4,则该扇形的面积为( )A、4π B、6π C、8π D、12π10. 如图M2-4,已知正方形ABCD的边长为4cm,动点P从A出发,沿AD边以1cm/s的速度运动,动点Q从B出发,沿BC-CD边以2cm/s的速度运动,点P,Q同时出发,运动到点D时均停止运动.设运动时间为x(单位:s),△BPQ的面积为y(单位:cm2),则y与x之间的函数图象大致是( ); A、
A、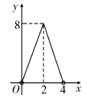 B、
B、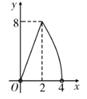 C、
C、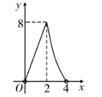 D、
D、
二、填空题(本大题6小题,每小题4分,共24分)
-
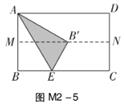
11. 一组数据3,5,9,5,7,8的中位数是 .12. 舌尖上的浪费让人触目惊心!据统计,中国每年浪费的粮食总量约为50 000 000吨,把50 000 000用科学记数法表示为 。13. 计算:2-2+( -1)+|-4|= .14. 平行四边形ABCD中,∠A+∠C=100°,则∠B= .15. 在反比例函数y= 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是 。16. 将矩形纸片ABCD按如图M2-5方式折叠,M,N分别为AB,CD的中点。若AB=20cm,AB<BC,则折痕AE的长为cm.
三、解答题(一)(本大题3小题,每小题6分,共18分)
-
17. 解不等式: ,并把它的解集表示在如图M2-6所示的数轴上
 18. 解分式方程: ,19. 某茶叶商店销售一批袋装茶叶,第一个月以50元/袋的价格售出80袋,第二个月以40元/袋的价格将这批茶叶全部售出,销售收入不超过8000元,这批茶叶最多有多少袋?
18. 解分式方程: ,19. 某茶叶商店销售一批袋装茶叶,第一个月以50元/袋的价格售出80袋,第二个月以40元/袋的价格将这批茶叶全部售出,销售收入不超过8000元,这批茶叶最多有多少袋?四、解答题(二)(本大题3小题,每小题7分,共21分)
-
20. 如图M2-7,在Rt△ABC中,∠ACB=90°,AC=12,AB=13.
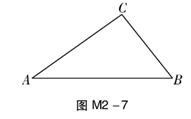 (1)、作△ABC的高CD;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,求CD的长.21. 如图M2-8,在菱形ABCD中,AB=2,∠ABC=60°,点O为对称中心,过点O的直线l交AD于点E,交BC于点F.
(1)、作△ABC的高CD;(要求:尺规作图,不写作法,保留作图痕迹)(2)、在(1)的条件下,求CD的长.21. 如图M2-8,在菱形ABCD中,AB=2,∠ABC=60°,点O为对称中心,过点O的直线l交AD于点E,交BC于点F. (1)、求证:△AOE≌△COF;(2)、当∠AOE=30°时,求线段EF的长度.22. 为做好食堂的服务工作,某学校食堂对学生最喜爱的菜肴进行了抽样调查。如图M2-9是根据收集的数据绘制的统计图(不完整):
(1)、求证:△AOE≌△COF;(2)、当∠AOE=30°时,求线段EF的长度.22. 为做好食堂的服务工作,某学校食堂对学生最喜爱的菜肴进行了抽样调查。如图M2-9是根据收集的数据绘制的统计图(不完整):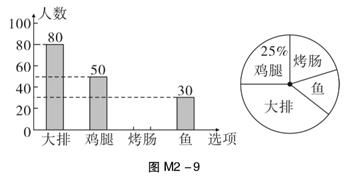 (1)、参加抽样调查的学生数是人,扇形统计图中“大排”部分的圆心角是 °;(2)、把条形统计图补充完整;(3)、若全校有3000名学生,请你根据以上数据估计最喜爱“烤肠”的学生人数。
(1)、参加抽样调查的学生数是人,扇形统计图中“大排”部分的圆心角是 °;(2)、把条形统计图补充完整;(3)、若全校有3000名学生,请你根据以上数据估计最喜爱“烤肠”的学生人数。五、解答题(三)(本大题3小题,每小题9分,共27分)
-
23. 已知:如图M2-10,抛物线y=ax2+x+c与x轴交于点A(-1,0),B(3,0).
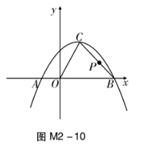 (1)、试确定该抛物线的函数表达式;(2)、已知点C是该抛物线的顶点,求△OBC的面积;(3)、若点P是线段BC上的一动点,求OP的最小值.24. 如图M2-11,Rt△ABC中,∠C=90°,BD为△ABC的角平分线,以AD为直径的⊙O交AB于点E,BD的延长线交⊙O于点F,连接AF,EF,ED.
(1)、试确定该抛物线的函数表达式;(2)、已知点C是该抛物线的顶点,求△OBC的面积;(3)、若点P是线段BC上的一动点,求OP的最小值.24. 如图M2-11,Rt△ABC中,∠C=90°,BD为△ABC的角平分线,以AD为直径的⊙O交AB于点E,BD的延长线交⊙O于点F,连接AF,EF,ED.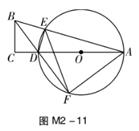 (1)、求证:∠BDC=∠BDE;(2)、求证:FA=FE;(3)、若BC=4,CD=3,求AF的长.25. 如图M2-12①,等边三角形ABC的边长为2,P是BC边上的任一点(与B,C不重合),设BP=x,连接AP,以AP为边向两侧作等边三角形APD和等边三角形APE,分别与边AB,AC交于点M,N.
(1)、求证:∠BDC=∠BDE;(2)、求证:FA=FE;(3)、若BC=4,CD=3,求AF的长.25. 如图M2-12①,等边三角形ABC的边长为2,P是BC边上的任一点(与B,C不重合),设BP=x,连接AP,以AP为边向两侧作等边三角形APD和等边三角形APE,分别与边AB,AC交于点M,N.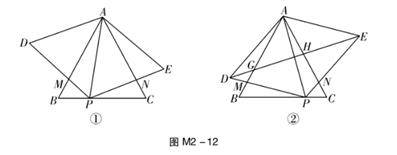 (1)、求证:AM=AN;(2)、求四边形ADPE与△ABC重叠部分的面积S与x之间的函数关系式及S的最小值;(3)、如图M2-12②,连接DE,分别与边AB,AC交于点G,H.当x为何值时,∠BAD=15°?
(1)、求证:AM=AN;(2)、求四边形ADPE与△ABC重叠部分的面积S与x之间的函数关系式及S的最小值;(3)、如图M2-12②,连接DE,分别与边AB,AC交于点G,H.当x为何值时,∠BAD=15°?