内蒙古通辽市2018-2019学年中考数学模拟考试试卷

试卷更新日期：2019-06-28 类型：中考模拟

进入出卷网下载

一、选择题（每题3分，共30分）

1. ﹣2019的倒数是（）

A、2019 B、 $\frac{1}{2019}$ C、﹣ $\frac{1}{2019}$ D、﹣2019

查看试题解析
2. 16的算术平方根为（）

A、 ±4 B、4 C、﹣4 D、8

查看试题解析
3. 下列四边形中，是中心对称而不是轴对称图形的是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
4. 如图1，该几何体是由5个棱长为1个单位长度的正方体摆放而成，将正方体A向右平移2个单位长度后（如图2），所得几何体的视图（）

A、主视图改变，俯视图改变 B、主视图不变，俯视图不变 C、主视图改变，俯视图不变 D、主视图不变，俯视图改变

查看试题解析
5. 下列说法正确的是（）

A、为了审核书稿中的错别字，选择抽样调查 B、为了了解春节联欢晚会的收视率，选择全面调查 C、“射击运动员射击一次，命中靶心”是随机事件 D、“经过有交通信号灯的路口，遇到红灯”是必然事件

查看试题解析
6. 如图，平行四边形ABCD中，BE⊥CD ， BF⊥AD ，垂足分别为E、F ， CE＝2，DF＝1，∠EBF＝60°，则这个平行四边形ABCD的面积是（）

A、2 $\sqrt{2}$ B、2 $\sqrt{6}$ C、3 $\sqrt{6}$ D、12 $\sqrt{3}$

查看试题解析
7. 当ab＞0时，y＝ax²与y＝ax＋b的图象大致是（）

A、 B、 C、 D、

查看试题解析
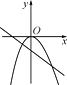8. 如图，线段CD两个端点的坐标分别为C（﹣1，﹣2），D（﹣2，﹣1），以原点O为位似中心，在第一象限内将线段CD扩大为原来的2倍，得到线段AB ，则线段AB的中点E的坐标为（）

A、（3，3） B、（ $\frac{3}{2} ， \frac{3}{2}$ ） C、（2，4） D、（4，2）

查看试题解析
9. 如图，在锐角三角形ABC中，BC＝4，∠ABC＝60°，BD平分∠ABC ，交AC于点D ， M ， N分别是BD ， BC上的动点，
则CM+MN的最小值是（）

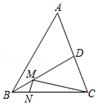A、 $\sqrt{3}$ B、2 C、2 $\sqrt{3}$ D、4

查看试题解析
10. 如图：二次函数y＝ax²+bx+c的图象所示，下列结论中：①abc＞0；②2a+b＝0；③当m≠1时，a+b＞am²+bm；④a﹣b+c＞0；⑤若ax₁²+bx₁＝ax₂²+bx₂ ，且x₁≠x₂ ，则x₁+x₂＝2，正确的个数为（）

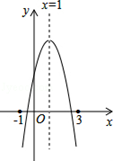A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题（每题3分，共21分）

11. 分解因式：a³b﹣ab³＝．

查看试题解析
12. 若菱形两条对角线的长分别是6cm和8cm ，则其面积为cm² ．

查看试题解析
13. 小丽计算数据方差时，使用公式S²＝ $\frac{1}{5}$ [（5﹣ $\bar{x}$ ）²+（8﹣ $\bar{x}$ ）²+（13﹣ $\bar{x}$ ）² $+ (14 - \bar{x})$ ²+（15﹣ $\bar{x}$ ）²]，则公式中 $\bar{x}$ ＝．

查看试题解析
14. 不等式 $\frac{3 x - 1}{2} > - 2$ 的最小整数解是．

查看试题解析
15. 如图，将半径为6的半圆，绕点A逆时针旋转75°，使点B落到点B′处，则图中阴影部分的面积是．

查看试题解析
16. 如图1，AF ， BE是△ABC的中线，AF⊥BE ，垂足为点P ，设BC＝a ， AC＝b ， AB＝c ，则a²+b²＝5c² ，利用这一性质计算．如图2，在平行四边形ABCD中，E ， F ， G分别是AD ， BC ， CD的中点，EB⊥EG于点E ， AD＝8，AB＝2 $\sqrt{5}$ ，则AF＝．

查看试题解析
17. 如图，已知正方形ABCD ，点M是边BA延长线上的动点（不与点A重合），且AM＜AB ， △CBE由△DAM平移得到．若过点E作EH⊥AC ， H为垂足，则有以下结论：①点M位置变化，使得∠DHC＝60°时，2BE＝DM；②无论点M运动到何处，都有DM＝ $\sqrt{2}$ HM；③无论点M运动到何处，∠CHM一定大于135°．其中正确结论的序号为．

查看试题解析

三、解答题（共10小题，共69分）

18. 计算：﹣1⁴+（2018﹣π）⁰-（- $\frac{1}{2}$ ）^-1+∣1- $\sqrt{3}$ ∣-2sin60°

查看试题解析
19.

(1)、实数x取哪些整数时，不等式2x﹣1＞x+1与 $\frac{1}{2}$ x﹣1≤7﹣ $\frac{3}{2}$ x都成立？

(2)、化简：（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 1}{x^{2} - 4 x + 4}$ ）÷ $\frac{x - 4}{x}$ ，并从0≤x≤4中选取一个合适的
整数代入求值．

查看试题解析
20. 某校260名学生参加植树活动，活动结束后学校随机调查了部分学生每人的植树棵数，并绘制成如下的统计图①和统计图②．请根据相关信息，解答下列问题：

(1)、本次接受调查的学生人数为，图①中m的值为；

(2)、求本次调查获取的样本数据的众数和中位数；

(3)、求本次调查获取的样本数据的平均数，并根据样本数据，估计这260名学生共植树多少棵？

查看试题解析
21. 如图，已知一次函数y₁＝k₁x+b的图象与x轴、y轴分别交于A ． B两点，与反比例函数y₂＝ $\frac{k^{2}}{x}$ 的图象分别交于C ． D两点，点D（2，﹣3），OA＝2．

(1)、求一次函数y₁＝k₁x+b与反比例函数y₂＝ $\frac{k^{2}}{x}$ 的解析式；

(2)、直接写出k₁x+b﹣ $\frac{k^{2}}{x}$ ≥0时自变量x的取值范围．

查看试题解析
22.
如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：

(1)、画出△ABC关于x轴对称的△A₁B₁C₁ ，并写出点A₁的坐标．

(2)、画出△A₁B₁C₁绕原点O旋转180°后得到的△A₂B₂C₂ ，并写出点A₂的坐标．

查看试题解析
23. 如图，已知A、F、C、D四点在同一条直线上，AF＝CD ， AB∥DE ，且AB＝DE ．

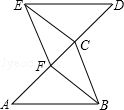(1)、求证：△ABC≌△DEF；

(2)、若EF＝3，DE＝4，∠DEF＝90°，请直接写出使四边形EFBC为菱形时AF的长度．

查看试题解析
24. 如图，一座山的一段斜坡BD的长度为600米，且这段斜坡的坡度i＝1：3（沿斜坡从B到D时，其升高的高度与水平前进的距离之比）．已知在地面B处测得山顶A的仰角为30°，在斜坡D处测得山顶A的仰角为45°．求山顶A到地面BC的高度AC是多少米？

查看试题解析
25. 设m ， n是任意两个实数，规定m ， n两数较大的数称作这两个数的“绝对最值”，用sec（m ， n）表示．例如：sec（﹣1，﹣2）＝﹣1，sec（1，2）＝2，sec（0，0）＝0，参照上面的材料，解答下列问题：

(1)、sec（π，3.14）＝， sec（﹣ $\frac{2018}{2019}$ ，﹣ $\frac{2017}{2018}$ ）＝；

(2)、若sec（﹣3x﹣1，x+1）＝﹣3x﹣1，求x的取值范围；

(3)、求函数y＝x²﹣2x﹣4与y＝﹣x+2的图象的交点坐标，函数y＝x²﹣2x﹣4图象如图所示，请你在图中作出函数y＝﹣x+2的图象，并根据图象直接写出sec（﹣x+2，x²﹣2x﹣4）的最小值．

查看试题解析
26. 如图，△ABC内接于⊙O ， AB是⊙O的直径，弦CD与AB交于点E ，连接AD ，过点A作直线MN ，使∠MAC＝∠ADC ．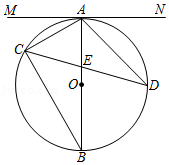

(1)、求证：直线MN是⊙O的切线．

(2)、若sin∠ADC＝ $\frac{1}{2}$ ，AB＝8，AE＝3，求DE的长．

查看试题解析
27. 如图，在平面直角坐标系中，二次函数y＝ax²+bx+c交x轴于点A（﹣4，0）、B（2，0），交y轴于点C（0，6），在y轴上有一点E（0，﹣2），连接AE ．

(1)、求二次函数的表达式；

(2)、若点D为抛物线在x轴负半轴上方的一个动点，求△ADE面积的最大值；

(3)、抛物线对称轴上是否存在点P ，使△AEP为等腰三角形？若存在，请直接写出所有P点的坐标，若不存在请说明理由．

查看试题解析