河北省保定市2018-2019学年中考数学模拟冲刺考试试卷
试卷更新日期：2019-06-28 类型：中考模拟
一、选择题（本大题共16个小题，共42分．1~10小题各3分；11~16小题各2分．）
-
1. 下列各式不成立的是（ ）A、-(-3)=3 B、|2|=|-2| C、0>|-1| D、-2>-32. 下列计算结果为x7的是（ ）A、x9-x2 B、x·x6 C、x14÷x2 D、(x4）33. 如图1，工程队要修建一条公路，从A村沿北偏东75°方向到B村，从B村沿北偏西25°方向到C村．若要保持公路CE与AB的方向一致，则∠ECB=（ ）
A、80° B、90° C、100° D、105°4. 若 是3-m的立方根，则（ ）A、m=3 B、m是小于3的实数 C、m是大于3的实数 D、m可以是任意实数5. 如图2，一个几何体由5个大小相同、棱长为1的小正方体搭成，下列关于这个几何体的说法正确的是（ ）
A、主视图的面积为5 B、左视图的面积为3 C、俯视图的面积为3正面 D、主视图、左视图和俯视图的面积都是46. 设“
”分别表示三种不同的物体，如图3，前两架天平保持平衡，如果要使第三架天平也平衡，那么“?”处全放“ 
”的个数为（ ） 
A、5 B、4 C、3 D、27. 如图4，点A，B，C在正方形网格中的格点上，每个小正方形的边长为1，则下列关于△ABC边长的说法，正确的是（ ）
A、AB，BC长均为有理数，AC长为无理数 B、AC长是有理数，AB，BC长均为无理数 C、AB长是有理数，AC，BC长均为无理数 D、三边长均为无理数8. 下列式子运算结果为x+1的是（ ）A、 B、1- C、 D、9. 某同学以正六边形三个不相邻的顶点为圆心，边长为半径，向外作三段圆弧，设计了如图5所示的图案。已知正六边形的边长为1，则该图案外围轮廓的周长为（ ）
A、2π B、3π C、4π D、6π10. 由下列两个点确定的直线经过原点的是（ ）A、(1，2)和（2，3） B、（-2，3)和（4，-6） C、（2，3）和（-4，6） D、（2，-3）和（-4，-6）11. 如图，C，E是直线l两侧的点，以点C为圆心，CE长为半径作圆弧交l于A，B两点；再分别以A，B为圆心，大于 AB的长为半径作圆弧，两弧交于点D，连接CA，CB，CD，下列结论不一定成立的是（ ）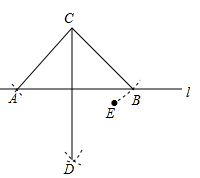
A、CD⊥l B、点A，B关于直线CD对称 C、CD平分∠ACB D、点C，D关于直线l对称12. 若点（x1 ， y1）、（x2 ， y2）都是反比例函数y= 图象上的点，且y1<0<y2 ， 则（ ）A、x1>x2 B、x1<x2 C、y随x的增大而减小 D、这两点有可能在同一象限13. 某工厂六台机床第一天和第二天生产的零件数分别如图7-1和图7-2所示，则与第一天相比，这六台机床第二天生产零件数的平均数与方差的变化是（ ）
A、平均数变大，方差不变 B、平均数变小，方差变大 C、平均数不变，方差变小 D、平均数不变，方差变大14. 某农场拟建两间矩形饲养室，一面靠足够长的墙体，中间用一道围栏隔开，并在如图8所示的三处各留1m宽的门，所有围栏的总长（不含门）为27m，则能建成的饲养室面积最大为（ ）
A、75m2 B、 m2 C、48m2 D、 m215. 把两个相同的矩形按图9所示的方式叠合起来，重叠部分是图中阴影区域，若AD=4，DC=3，则重叠部分的面积为（ ）
A、6 B、 C、 D、16. 已知关于x的一元二次方程（a+1)x2+2bx+(a+1)=0有两个相等的实数根，则下列说法正确的是（ ）A、1一定不是方程x2+bx+a=0的根 B、0一定不是方程x2+bx+a=0的根 C、-1可能是方程x2+bx+a=0的根 D、1和-1都是方程x2+bx+a=0的根二、填空题（本大题有3个小题，共12分．17~18小题各3分；19小题有2个空，每空3分．）
-
17. 计算： = ．18. 一个矩形的两边长分别为a，b，其周长为14，面积是12，则ab2+a2b的值为 ．19. 如图10，在△ABC中，AB>AC，∠B=45°，AC=5，BC=4 ，则AB的长为 ；若E是AB边上一点，将△BEC沿EC所在直线翻折得到△DEC，DC交AB于F，则当DE∥AC时，tan∠BCD的值为 ．
三、解答题（本大题共7个小题，共66分．）
-
20. 李华同学准备化简：（3x2-5x-3）-（x2+2x□6)，算式中“□”是“+，-，×，÷”中的某一种运算符号．(1)、如果“□”是“÷”，请你化简：（3x2-5x-3）-（x2+2x÷6)；(2)、当x=1时，（3x2-5x-3）-(x2+2x□6)的结果是-2，请你通过计算说明“□”所代表的运算符号．21. 某校380名学生参加了这学期的“读书伴我行”活动，要求每人在这学期读书4~7本，活动结束后随机抽查了20名学生每人的读书量，并分为四种等级，A：4本；B：5本；C：6本；D：7本．将各等级的人数绘制成尚不完整的扇形图（如图11-1）和条形图（如图11-2）．
回答下列问题：
(1)、补全条形图；这20名学生每人这学期读书量的众数是本，中位数是本；(2)、在求这20名学生这学期每人读书量的平均数时，小亮是这样计算的：=5.5（本）．
小亮的计算是否正确?如果正确，估计这380名学生在这学期共读书多少本；如果不正确，请你帮他计算出正确的平均数，并估计这380名学生在这学期共读书多少本；
(3)、若A等级的四名学生中有男生、女生各两名，现从中随机选出两名学生写读书感想，请用画树状图的方法求出刚好选中一名男生、一名女生的概率。22. 观察下列两个等式：2- =2× +1，5- =5x +1，给出定义如下：
我们称使等式a-b=ab+1成立的一对有理数“a，b”为“共生有理数对”，记为（a，b)，
(1)、通过计算判断数对“-2，1”，“4， ”是不是“共生有理数对”；(2)、若（6，a)是“共生有理数对”，求a的值；(3)、若（m，n)是“共生有理数对”，则“-n，-m”“共生有理数对”（填“是”或“不是”），并说明理由；(4)、如果(m，n)是“共生有理数对”（其中n≠1)，直接用含n的代数式表示m．23. 如图12-1，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE=40°，连接BD，CE，将△ADE绕点A旋转，BD，CE也随之运动．
(1)、求证：BD=CE；(2)、在△ADE绕点A旋转过程中，当AE∥BC时，求∠DAC的度数；(3)、如图12-2，当点D恰好是△ABC的外心时，连接DC，判断四边形ADCE的形状，并说明理由．24. 甲、乙两车沿相同路线从A城出发前往B城．已知A、B两城之间的距离是300km，甲车8：30出发，速度为60km/h；乙车9：30出发，速度为100km/h．设甲、乙两车离开A城的距离分别为y1 ， y2(单位：km)，甲车行驶x（h)．(1)、分别写出y1 ， y2与x之间的函数关系式，并直接写出x的取值范围；(2)、当甲车出发1.5小时时，求甲车与乙车之间的距离；(3)、在乙车行驶过程中：①求乙车没有超过甲车时x的取值范围；
②直接写出甲车与乙车之间的距离是40km时x的值．
25. 如图13，在矩形ABCD中，AB=4，BC=3，点M是AB边上一点，且∠CMB=45°，点Q是直线AB上一点且在点B的右侧，BQ=4，点P从点Q出发，沿射线QA方向以每秒1个单位长度的速度运动，设运动时间为t秒．以P为圆心，PC为半径作半圆P，交直线AB分别于点G，H(点G在H的左侧）．
（参考数据：sin37°= ，sin53°= ，tan37°= ）
(1)、当t=3秒时，PC的长等于 ，t=秒时，半圆P与AD相切；(2)、当点P与点B重合时，求半圆P被矩形ABCD的对角线AC所截得的弦长；(3)、若∠MCP=15°，求扇形HPC的面积26. 已知点P(2，-3）在抛物线L：y=ax2-2ax+a+k(a，k均为常数且a≠0）上，L交y轴于点C，连接CP．
(1)、用a表示k，并求L的对称轴；(2)、当L经过点（4，-7)时，求此时L的表达式及其顶点坐标；(3)、横，纵坐标都是整数的点叫做整点．如图14，当a<0时，若L在点C，P之间的部分与线段CP所围成的区域内（不含边界）恰有5个整点，求a的取值范围；(4)、点M(x1 ， y1），N(x2 ， y2）是L上的两点，若t≤x1≤t+1，当x2≥3时，均有y1≥y2 ， 直接写出t的取值范围．