2016-2017学年重庆市沙坪坝区四校联盟八年级下学期期中数学试卷
试卷更新日期:2017-06-02 类型:期中考试
一、选择题
-
1. 下列各点中位于第四象限的点是( )A、(3,4) B、(﹣3,4) C、(3,﹣4) D、(﹣3,﹣4)2. 下列各曲线中表示y是x的函数的是( )A、
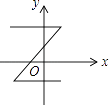 B、
B、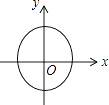 C、
C、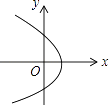 D、
D、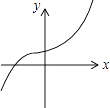 3. 函数y= 中,自变量x的取值范围是( )A、x>4 B、x≥2 C、x≥2且x≠﹣4 D、x≠﹣44. 函数y=kx+1与函数y= 在同一坐标系中的大致图象是( )A、
3. 函数y= 中,自变量x的取值范围是( )A、x>4 B、x≥2 C、x≥2且x≠﹣4 D、x≠﹣44. 函数y=kx+1与函数y= 在同一坐标系中的大致图象是( )A、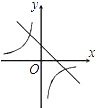 B、
B、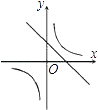 C、
C、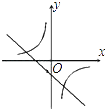 D、
D、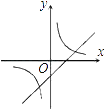 5. 已知正比例函数y=(m+1)x,y随x的增大而减小,则m的取值范围是( )A、m<﹣1 B、m>﹣1 C、m≥﹣1 D、m≤﹣16. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )A、1:2:3:4 B、1:2:2:1 C、1:2:1:2 D、1:1:2:27. 在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )A、AB∥DC,AD=BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD∥BC8. 矩形边长为10cm和15cm,其中一内角平分线把长边分为两部分,这两部分是( )A、6cm和9cm B、7cm和8 cm C、5cm和10cm D、4cm和11cm9. 已知直线y=(m﹣3)x﹣3m+1不经过第一象限,则m的取值范围是( )A、m≥ B、m≤ C、 ≤m<3 D、 ≤m≤310. 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
5. 已知正比例函数y=(m+1)x,y随x的增大而减小,则m的取值范围是( )A、m<﹣1 B、m>﹣1 C、m≥﹣1 D、m≤﹣16. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是( )A、1:2:3:4 B、1:2:2:1 C、1:2:1:2 D、1:1:2:27. 在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )A、AB∥DC,AD=BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD∥BC8. 矩形边长为10cm和15cm,其中一内角平分线把长边分为两部分,这两部分是( )A、6cm和9cm B、7cm和8 cm C、5cm和10cm D、4cm和11cm9. 已知直线y=(m﹣3)x﹣3m+1不经过第一象限,则m的取值范围是( )A、m≥ B、m≤ C、 ≤m<3 D、 ≤m≤310. 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )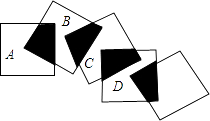 A、2cm2 B、4cm2 C、6cm2 D、8cm211. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )
A、2cm2 B、4cm2 C、6cm2 D、8cm211. 如图,P是边长为1的正方形ABCD的对角线BD上的一点,点E是AB的中点,则PA+PE的最小值是( )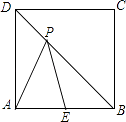 A、 B、 C、 D、12. 如图,点A是双曲线y= 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
A、 B、 C、 D、12. 如图,点A是双曲线y= 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( ) A、y= B、y= C、y=﹣ D、y=﹣
A、y= B、y= C、y=﹣ D、y=﹣二、填空题
-
13. 已知点P的坐标为(﹣5,﹣8),那么该点P到x轴的距离为 .14. 在函数y=(k>0的常数)的图象上有三个点(-2,y1),(-1,y2),( , y3),函数值y1 , y2 , y3的大小为 .
15. 如图,在▱ABCD中,EF经过对角线的交点O,交AB于点E,交CD于点F.若AB=5,AD=4,OF=1.8,那么四边形BCFE的周长为 .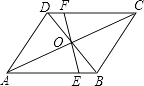 16. 方程组 的解是 .
16. 方程组 的解是 .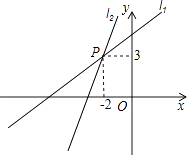 17. 波波和爸爸两人以相同路线从家出发,步行前往公园.图中OA、BC分别表示爸爸和波波所走的路程y(米)与爸爸步行的时间x(分)的函数图象,已知爸爸从家步行到公园所花的时间比波波的2倍还多10分钟.则在步行过程中,他们父子俩相距的最远路程是米.
17. 波波和爸爸两人以相同路线从家出发,步行前往公园.图中OA、BC分别表示爸爸和波波所走的路程y(米)与爸爸步行的时间x(分)的函数图象,已知爸爸从家步行到公园所花的时间比波波的2倍还多10分钟.则在步行过程中,他们父子俩相距的最远路程是米. 18. 如图,正方形ABCD的对角线AC、BD相交于点O,∠CAB的平分线交BD于点E,交BC于点F.若OE=1,则CF= .
18. 如图,正方形ABCD的对角线AC、BD相交于点O,∠CAB的平分线交BD于点E,交BC于点F.若OE=1,则CF= .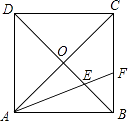
三、解答题
-
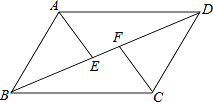
19. 已知y与x成一次函数,当x=0时,y=3,当x=2时,y=7.(1)、写出y与x之间的函数关系式.(2)、当x=4时,求y的值.20. 如图,在▱ABCD中,E、F为对角线BD上的两点,且BE=DF.求证:∠BAE=∠DCF.
四、解答题
-
21. 已知直线l1:y1=2x+3与直线l2:y2=kx﹣1交于A点,A点横坐标为﹣1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.
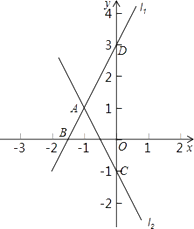 (1)、求出A点坐标及直线l2的解析式;(2)、连接BC,求出S△ABC .22. 如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.问四边形AFCE是菱形吗?请说明理由.
(1)、求出A点坐标及直线l2的解析式;(2)、连接BC,求出S△ABC .22. 如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F.问四边形AFCE是菱形吗?请说明理由.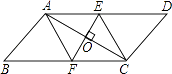 23. 如图,已知A(﹣4,2)、B(a,﹣4)是一次函数y=kx+b的图象与反比例函数y= 的图象的两个交点;
23. 如图,已知A(﹣4,2)、B(a,﹣4)是一次函数y=kx+b的图象与反比例函数y= 的图象的两个交点; (1)、求一次函数的解析式;(2)、根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;(3)、求△AOB的面积.24. 快、慢两车分别从相距480km路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1h,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路y km与所用时间x h之间的函数图象如图,请结合图象信息解答下列问题:
(1)、求一次函数的解析式;(2)、根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;(3)、求△AOB的面积.24. 快、慢两车分别从相距480km路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1h,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路y km与所用时间x h之间的函数图象如图,请结合图象信息解答下列问题: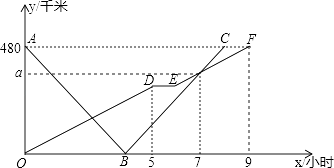 (1)、直接写出慢车的行驶速度和a的值;(2)、求快车的速度和B点坐标;(3)、快车与慢车第一次相遇时,距离甲地的路程是多少千米?25. 如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”.例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”,再加22,545,3883,345543,…,都是“和谐数”.(1)、请你直接写出3个四位“和谐数”;请你猜想任意一个四位“和谐数”能否被11整除?并说明理由;(2)、已知一个能被11整除的三位“和谐数”,设其个位上的数字x(1≤x≤4,x为自然数),十位上的数字为y,求y与x的函数关系式.26.
(1)、直接写出慢车的行驶速度和a的值;(2)、求快车的速度和B点坐标;(3)、快车与慢车第一次相遇时,距离甲地的路程是多少千米?25. 如果把一个自然数各数位上的数字从最高位到个位依次排出的一串数字,与从个位到最高位依次排出的一串数字完全相同,那么我们把这样的自然数称为“和谐数”.例如自然数12321,从最高位到个位依次排出的一串数字是:1,2,3,2,1,从个位到最高位依次排出的一串数字仍是:1,2,3,2,1,因此12321是一个“和谐数”,再加22,545,3883,345543,…,都是“和谐数”.(1)、请你直接写出3个四位“和谐数”;请你猜想任意一个四位“和谐数”能否被11整除?并说明理由;(2)、已知一个能被11整除的三位“和谐数”,设其个位上的数字x(1≤x≤4,x为自然数),十位上的数字为y,求y与x的函数关系式.26.已知点F是等边△ABC的边BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与等边△ABC在BC的同侧,且CD∥AB,连结BE.
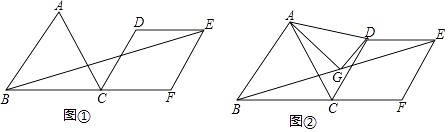 (1)、如图①,若AB=10,EF=8,请计算△BEF的面积;(2)、如图②,若点G是BE的中点,连接AG、DG、AD.试探究AG与DG的位置和数量关系,并说明理由.
(1)、如图①,若AB=10,EF=8,请计算△BEF的面积;(2)、如图②,若点G是BE的中点,连接AG、DG、AD.试探究AG与DG的位置和数量关系,并说明理由.