2016-2017学年浙江省杭州市大江东区八年级下学期期中数学试卷

试卷更新日期：2017-06-02 类型：期中考试

进入出卷网下载

一、仔细选一选

1. 若二次根式 $\sqrt{x - 1}$ 有意义，则x的取值范围是（）

A、x＞1 B、x≥1 C、x＜1 D、x≤1

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $3 \sqrt{2} - \sqrt{8} = \sqrt{2}$ D、 $3 + \sqrt{3} = 3 \sqrt{3}$

查看试题解析
3. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 一元二次方程x²﹣4x﹣6=0，经过配方可变形为（）

A、（x﹣2）²=10 B、（x﹣2）²=6 C、（x﹣4）²=6 D、（x﹣2）²=2

查看试题解析
5. 温州某服装店十月份的营业额为8000元，第四季度的营业额共为40000元．如果平均每月的增长率为x，则由题意可列出方程为（）

A、8000（1+x）²=40000 B、8000+8000（1+x）²=40000 C、8000+8000×2x=40000 D、8000[1+（1+x）+（1+x）²]=40000

查看试题解析
6. 已知平行四边形ABCD的对角钱AC与BD相交于点O，BD⊥AC，若AB=6，AC=8，则对角线BD的长是（）

A、2 $\sqrt{2}$ B、2 $\sqrt{5}$ C、4 $\sqrt{2}$ D、4 $\sqrt{5}$

查看试题解析
7. 关于x的一元二次方程（k﹣1）x²﹣2x+3=0有两个不相等的实根，则k的取值范围是（）

A、k＜ $\frac{4}{3}$ B、k＜ $\frac{4}{3}$ 且k≠1 C、0≤k≤ $\frac{4}{3}$ D、k≠1

查看试题解析
8. 已知：一组数据x₁ ， x₂ ， x₃ ， x₄ ， x₅的平均数是2，方差是 $\frac{1}{3}$ ，那么另一组数据3x₁﹣2，3x₂﹣2，3x₃﹣2，3x₄﹣2，3x₅﹣2的平均数和方差分别是（）

A、2， $\frac{1}{3}$ B、2，1 C、4， $\frac{2}{3}$ D、4，3

查看试题解析
9. 如图，在平行四边形ABCD中，点A₁ ， A₂ ， A₃ ， A₄和C₁ ， C₂ ， C₃ ， C₄分别是ABCD的五等分点，点B₁ ， B₂和D₁ ， D₂分别是BC和DA的三等分点，已知四边形A₄B₂C₄D₂的面积为2，则平行四边形ABCD的面积为（）

A、4 B、 $\frac{3}{10}$ C、 $\frac{10}{3}$ D、30

查看试题解析
10. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论：（1）∠DCF= $\frac{1}{2}$ ∠BCD，（2）EF=CF；（3）S_△_BEC=2S_△_CEF；（4）∠DFE=3∠AEF，其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、认真填一填

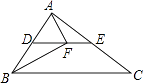
11. 当a=﹣3时，二次根式 $\sqrt{1 - a}$ 的值是．

查看试题解析
12. 已知m是方程x²﹣x﹣2=0的一个实数根，则代数式 $(m^{2} - m) (m - \frac{2}{m} + 1)$ 的值为．

查看试题解析
13. 在证明命题“一个三角形中至少有一个内角不大于60°”成立时，我们利用反证法，先假设，则可推出三个内角之和大于180°，这与三角形内角和定理相矛盾．

查看试题解析
14. 如图所示，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=5，BC=8，则EF的长为．

查看试题解析
15.
如图，在平面直角坐标系xOy中，多边形OABCDE的顶点坐标为O（0，0），A（2，0），B（2，2），C（4，2），D（4，4），E（0，4），若如图过点M（1，2）的直线MP（与y轴交于点P）将多边形OABCDE分割成面积相等的两部分，则直线MP的函数表达式是．

查看试题解析
16. 在平面直角坐标系XOY中，有A（3，2），B （﹣1，﹣4 ），P是X轴上的一点，Q是Y轴上的一点，若以点A，B，P，Q四个点为顶点的四边形是平行四边形，则Q点的坐标是．

查看试题解析

三、全面答一答

17. 计算下列各式

(1)、 $\sqrt{24}$ ÷ $\sqrt{3}$ ﹣ $\sqrt{\frac{2}{3}}$ ×|﹣ $\sqrt{3}$ |+ ${(\sqrt{2} - 1)}^{0}$

(2)、 ${(\sqrt{3} + 1)}^{2}$ ﹣ $\sqrt{{(- 5)}^{2}}$ + ${}^{3}{\sqrt{- 64}}$ ．

查看试题解析
18. 解方程：

(1)、3x²﹣7x=0

(2)、（x﹣2）（2x﹣3）=2（x﹣2）

查看试题解析
19. 下面的表格是李刚同学一学期数学成绩的记录，根据表格提供的信息回答下面的问题
考试类别
平时
期中考试
期末考试
第一单元
第二单元
第三单元
第四单元
成绩
88
86
90
92
90
96

(1)、李刚同学6次成绩众数是．

(2)、李刚同学6次成绩的中位数是．

(3)、李刚同学平时成绩的平均数是．

(4)、如果用下图的权重给李刚打分，他应该得多少分？（满分100分，写出解题过程）

查看试题解析
20. 已知关于x的一元二次方程（a+c）x²+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．

(1)、如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；

(2)、如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；

(3)、如果△ABC是等边三角形，试求这个一元二次方程的根．

查看试题解析
21. 如图，在▱ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．

(1)、试说明：AE⊥BF；

(2)、判断线段DF与CE的大小关系，并予以说明．

查看试题解析
22. 某专业街有店面房共195间.2010年平均每间店面房的年租金为10万元；由于物价上涨，到2012年平均每间店面房的年租金上涨到了12.1万元．

(1)、求2010年至2012年平均每间店面房年租金的平均增长率；

(2)、据预测，当每间的年租金定为12.1万元时，195间店面房可全部租出；若每间的年租金每增加1万元，就要少租出10间．该专业街管委会要为租出的商铺每间每年交各种费用1.1万元，未租出的商铺每间每年交各种费用5000元．问当每间店面房的年租金上涨多少万元时，该专业街的年收益（收益=租金﹣各种费用）为2305万元？

查看试题解析
23.
如图，在平面直角坐标系中，点A，B的坐标分别是（﹣3，0），（0，6），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造▱PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．

(1)、当点C运动到线段OB的中点时，求t的值及点E的坐标；

(2)、当点C在线段OB上时，求证：四边形ADEC为平行四边形；

(3)、在线段PE上取点F，使PF=2，过点F作MN⊥PE，截取FM= $\sqrt{3}$ ，FN=1，且点M，N分别在第一、四象限，在运动过程中，当点M，N中，有一点落在四边形ADEC的边上时，直接写出所有满足条件的t的值．

查看试题解析

考试类别	平时				期中考试	期末考试
考试类别	第一单元	第二单元	第三单元	第四单元	期中考试	期末考试
成绩	88	86	90	92	90	96