2016-2017学年四川省广安市岳池县八年级下学期期中数学试卷

试卷更新日期：2017-06-02 类型：期中考试

进入出卷网下载

一、选择题

1. 下列式子中，属于最简二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt{1.2}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 要使二次根式 $\sqrt{x - 2}$ 有意义，x必须满足（）

A、x≤2 B、x≥2 C、x＞2 D、x＜2

查看试题解析
3. 下列算式计算正确的是（）

A、3 $\sqrt{2}$ ﹣ $\sqrt{2}$ =3 B、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ C、2 $\sqrt{3}$ ×3 $\sqrt{3}$ =6 $\sqrt{3}$ D、 $\sqrt{121 \div 4}$ = $\sqrt{121}$ ÷ $\sqrt{4}$ = $\frac{11}{2}$

查看试题解析
4. 若一个四边形的两条对角线相等，则称这个四边形为对角线四边形．下列图形不是对角线四边形的是（）

A、平行四边形 B、矩形 C、正方形 D、等腰梯形

查看试题解析
5. 适合下列条件的△ABC中，直角三角形的个数为（　　）
①a=3，b=4，c=5；
②a=6，∠A=45°；
③a=2，b=2，c=2 $\sqrt{2}$ ；
④∠A=38°，∠B=52°．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在△ABC中，AB=6，AC=10，点D，E，F分别是AB，BC，AC的中点，则四边形ADEF的周长为（）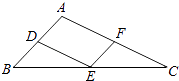

A、8 B、10 C、12 D、16

查看试题解析
7. 如图，在菱形ABCD中，AB=5，∠B：∠BCD=1：2，则对角线AC等于（）

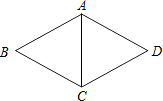A、5 B、10 C、15 D、20

查看试题解析
8. 小明在学习了正方形之后，给同桌小文出了道题，从下列四个条件：①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD中选两个作为补充条件，使▱ABCD为正方形（如图），现有下列四种选法，你认为其中错误的是（）

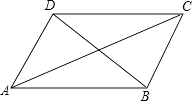A、①② B、②③ C、①③ D、②④

查看试题解析
9. 如图，小明同学在将一张矩形纸片ABCD的四个角向内折起时，发现恰好能拼成一个无缝隙无重叠的四边形EFGH．于是他测量出EH=12cm，EF=16cm，根据这两个数据他很快求出了边AD的长，则边AD的长是（）

A、12cm B、16cm C、20cm D、28cm

查看试题解析
10.
如图，在矩形ABCD中，AD= $\sqrt{2}$ AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；
②OE=OD；
③BH=HF；
④BC﹣CF=2HE；
⑤AB=HF．
其中正确的有（）

A、①②③④⑤ B、①②③④ C、①③④⑤ D、①②③⑤

查看试题解析

二、填空题

11. 计算： $\frac{\sqrt{18} - \sqrt{8}}{2}$ = ．

查看试题解析
12. 若 $\sqrt{{(x - 3)}^{2}}$ =3﹣x，则x的取值范围是．

查看试题解析
13. 若a+ $\frac{1}{a}$ = $\sqrt{10}$ ，则a﹣ $\frac{1}{a}$ = ．

查看试题解析
14. 已知a、b、c是三角形的三边长，如果满足（a﹣6）²+ $\sqrt{b - 8}$ +|c﹣10|=0，则三角形的形状是．

查看试题解析
15. 如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为 cm² ．

查看试题解析
16. 在平面直角坐标系中有以下几点：A（0，0），B（2，3），C（4，0），若以A、B、C为顶点，作一个平行四边形，请写出第四个顶点的位置坐标．

查看试题解析
17. 如图，在平面直角坐标系中，将矩形AOCD沿直线AE折叠（点E在边DC上），折叠后端点D恰好落在边OC上的点F处．若点D的坐标为（10，8），则点E的坐标为．

查看试题解析
18. 我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1））．图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S₁、S₂、S₃ ．若正方形EFGH的边长为2，则S₁+S₂+S₃= ．

查看试题解析

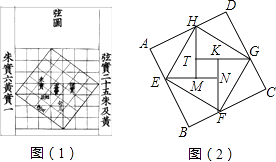
三、解答题

19. 计算下列各式：

(1)、2 $\sqrt{12}$ +6 $\sqrt{\frac{1}{3}}$ ﹣3 $\sqrt{48}$

(2)、 $\frac{2}{3}$ $\sqrt{9 x}$ +6 $\sqrt{\frac{x}{4}}$ ﹣2x $\sqrt{\frac{1}{x}}$ ．

查看试题解析
20. 计算下列各题：

(1)、 $\sqrt{8}$ +|1﹣ $\sqrt{2}$ |﹣π⁰+ ${(\frac{1}{2})}^{- 1}$

(2)、（ $\sqrt{8}$ + $\sqrt{3}$ ）× $\sqrt{6}$ ﹣（4 $\sqrt{2}$ ﹣3 $\sqrt{6}$ ）÷2 $\sqrt{2}$ ．

查看试题解析
21. 根据题意解答

(1)、已知x= $\sqrt{3}$ +1，y= $\sqrt{3}$ ﹣1，求下列各式的值．
①x²+2xy+y²
②x²﹣y²

(2)、先化简，再求值： $\frac{2 a}{a^{2} - 4}$ ÷（ $\frac{a^{2}}{a - 2}$ ﹣a），其中a= $\sqrt{3}$ ﹣2．

查看试题解析
22. 求证四边形AECF是平行四边形．

查看试题解析
23. 四边形ABCD是菱形，对角线AC=8cm，BD=6cm，DH⊥AB于H，求DH的长．

查看试题解析
24. 张倩同学打算制作一个平行四边形纸板，但手中只有一块等腰三角形纸板．张倩同学想了一下，用剪刀只剪了一刀，便得到一个平行四边形，且纸板充分利用没有浪费．你知道张倩是怎样剪的吗？用虚线表示出剪刀线；并请你画出两种张倩所拼的平行四边形．

查看试题解析
25. 如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．

(1)、求证：∠ADB=∠CDB；

(2)、若∠ADC=90°，求证：四边形MPND是正方形．

查看试题解析
26. 如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=26cm，动点P从点A出发，以1cm/s的速度向点D运动；动点Q从点C同时出发，以3cm/s的速度向点B运动．规定当其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t，求：

(1)、当t为何值时，PQ∥CD？

(2)、当t为何值时，PQ=CD？

查看试题解析
27. 如图，以△ABC的三边为边分别作等边△ACD、△ABE、△BCF

(1)、求证：△EBF≌△DFC；

(2)、求证：四边形AEFD是平行四边形；

(3)、①△ABC满足时，四边形AEFD是菱形．（无需证明）
②△ABC满足时，四边形AEFD是矩形．（无需证明）
③△ABC满足时，四边形AEFD是正方形．（无需证明）

查看试题解析