湖北省荆门市2019年中考数学试卷
试卷更新日期:2019-06-27 类型:中考真卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 的倒数的平方是( )A、2 B、 C、 D、2. 已知一天有86400秒,一年按365天计算共有31536000秒.用科学记数法表示31536000正确的是( )A、 B、 C、 D、3. 已知实数x,y满足方程组 则 的值为( )A、 B、 C、 D、4. 将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则 的度数是( )
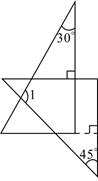 A、 B、 C、 D、5. 抛物线 与坐标轴的交点个数为( )A、0 B、1 C、2 D、36. 不等式组 的解集为( )A、 B、 C、 D、7. 投掷一枚质地均匀的骰子两次,向上一面的点数依次记为 .那么方程 有解的概率是( )A、 B、 C、 D、8. 欣欣服装店某天用相同的价格 卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )A、盈利 B、亏损 C、不盈不亏 D、与售价 有关9. 如果函数 ( 是常数)的图象不经过第二象限,那么 应满足的条件是( )A、 且 B、 且 C、 且 D、 且10. 如图, 的斜边在 轴上, ,含 角的顶点与原点重合,直角顶点 在第二象限,将 绕原点顺时针旋转 后得到 ,则 点的对应点 的坐标是( )
A、 B、 C、 D、5. 抛物线 与坐标轴的交点个数为( )A、0 B、1 C、2 D、36. 不等式组 的解集为( )A、 B、 C、 D、7. 投掷一枚质地均匀的骰子两次,向上一面的点数依次记为 .那么方程 有解的概率是( )A、 B、 C、 D、8. 欣欣服装店某天用相同的价格 卖出了两件服装,其中一件盈利20%,另一件亏损20%,那么该服装店卖出这两件服装的盈利情况是( )A、盈利 B、亏损 C、不盈不亏 D、与售价 有关9. 如果函数 ( 是常数)的图象不经过第二象限,那么 应满足的条件是( )A、 且 B、 且 C、 且 D、 且10. 如图, 的斜边在 轴上, ,含 角的顶点与原点重合,直角顶点 在第二象限,将 绕原点顺时针旋转 后得到 ,则 点的对应点 的坐标是( )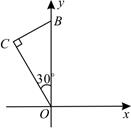 A、 B、 C、 D、11. 下列运算不正确的是( )A、
A、 B、 C、 D、11. 下列运算不正确的是( )A、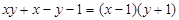 B、
C、
D、
12. 如图, 内心为 ,连接 并延长交 的外接圆于 ,则线段 与 的关系是( )
B、
C、
D、
12. 如图, 内心为 ,连接 并延长交 的外接圆于 ,则线段 与 的关系是( )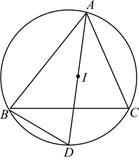 A、 B、 C、 D、不确定
A、 B、 C、 D、不确定二、填空题:本题共5小题,每小题3分,共15分。
-
13. 计算 .14. 已知 是关于 的方程 的两个不相等实数根,且满足 ,则 的值为.15. 如图,在平面直角坐标系中,函数 的图象与等边三角形 的边 , 分别交于点 , ,且 ,若 ,那么点 的横坐标为.
 16. 如图,等边三角形 的边长为2,以 为圆心,1为半径作圆分别交 边于 ,再以点 为圆心, 长为半径作圆交 边于 ,连接 ,那么图中阴影部分的面积为.
16. 如图,等边三角形 的边长为2,以 为圆心,1为半径作圆分别交 边于 ,再以点 为圆心, 长为半径作圆交 边于 ,连接 ,那么图中阴影部分的面积为.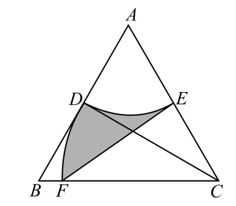 17. 抛物线 ( 为常数)的顶点为 ,且抛物线经过点 , , .下列结论:
17. 抛物线 ( 为常数)的顶点为 ,且抛物线经过点 , , .下列结论:① ,② ,③ ④ 时,存在点 使 为直角三角形.其中正确结论的序号为.
三、解答题:共69分。
-
18. 先化简,再求值:
,其中 .
19. 如图,已知平行四边形 中, . (1)、求平行四边形 的面积;(2)、求证: .20. 高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图.其中条形统计图因为破损丢失了阅读5册书数的数据.
(1)、求平行四边形 的面积;(2)、求证: .20. 高尔基说:“书,是人类进步的阶梯.”阅读可以丰富知识、拓展视野、充实生活等诸多益处.为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图.其中条形统计图因为破损丢失了阅读5册书数的数据.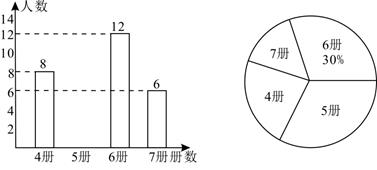 (1)、求条形图中丢失的数据,并写出阅读书册数的众数和中位数;(2)、根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;(3)、若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?21. 已知锐角 的外接圆圆心为 ,半径为 .
(1)、求条形图中丢失的数据,并写出阅读书册数的众数和中位数;(2)、根据随机抽查的这个结果,请估计该校1200名学生中课外阅读5册书的学生人数;(3)、若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?21. 已知锐角 的外接圆圆心为 ,半径为 .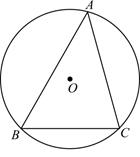 (1)、求证: ;(2)、若 中 ,求 的长及 的值.22. 如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 .
(1)、求证: ;(2)、若 中 ,求 的长及 的值.22. 如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 .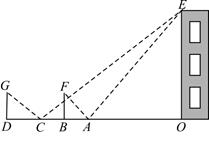 23. 为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据市场调查,在草莓上市销售的30天中,其销售价格 (元/公斤)与第 天之间满足 ( 为正整数),销售量 (公斤)与第 天之间的函数关系如图所示:
23. 为落实“精准扶贫”精神,市农科院专家指导李大爷利用坡前空地种植优质草莓.根据市场调查,在草莓上市销售的30天中,其销售价格 (元/公斤)与第 天之间满足 ( 为正整数),销售量 (公斤)与第 天之间的函数关系如图所示:
如果李大爷的草莓在上市销售期间每天的维护费用为80元.
(1)、求销售量 与第 天之间的函数关系式;(2)、求在草莓上市销售的30天中,每天的销售利润 与第 天之间的函数关系式;(日销售利润=日销售额-日维护费)(3)、求日销售利润 的最大值及相应的 .24. 已知抛物线 顶点 ,经过点 ,且与直线 交于 两点.(1)、求抛物线的解析式;(2)、若在抛物线上恰好存在三点 ,满足 ,求 的值;(3)、在 之间的抛物线弧上是否存在点 满足 ?若存在,求点 的横坐标,若不存在,请说明理由.(坐标平面内两点 之间的距离 )