湖北省鄂州市2019年中考数学试卷
试卷更新日期:2019-06-27 类型:中考真卷
一、选择题(每小题3分,共30分)
-
1. -2019的绝对值是( )A、2019 B、-2019 C、 D、2. 下列运算正确的是( )A、a3·a2=a6 B、a7÷a3=a4 C、(-3a)2=-6a2 D、(a-1)2=a2-13. 据统计,2019年全国高考人数再次突破千万,高达1031万人.数据1031万用科学记数法可表示为( )A、0.1031×106 B、1.031×107 C、1.031×108 D、10.31×1094. 如图是由7个小正方体组合成的几何体,则其左视图为( )
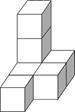 A、
A、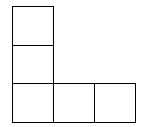 B、
B、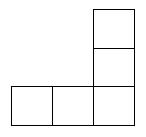 C、
C、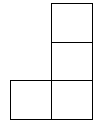 D、
D、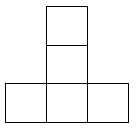 5. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=35o , 则∠1的度数为( )
5. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=35o , 则∠1的度数为( )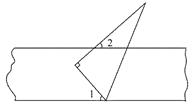 A、45o B、55o C、65o D、75o6. 已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为( )A、3 B、4.5 C、5.2 D、67. 关于x的一元二次方程x2-4x+m=0的两实数根分别为x1、x2 , 且x1+3x2=5,则m的值为( )A、
A、45o B、55o C、65o D、75o6. 已知一组数据为7,2,5,x,8,它们的平均数是5,则这组数据的方差为( )A、3 B、4.5 C、5.2 D、67. 关于x的一元二次方程x2-4x+m=0的两实数根分别为x1、x2 , 且x1+3x2=5,则m的值为( )A、 B、
C、
D、0
B、
C、
D、0  8. 在同一平面直角坐标系中,函数 与 (k为常数,且k≠0)的图象大致是( )A、
8. 在同一平面直角坐标系中,函数 与 (k为常数,且k≠0)的图象大致是( )A、 B、
B、 C、
C、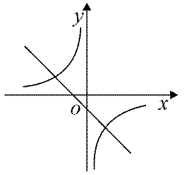 D、
D、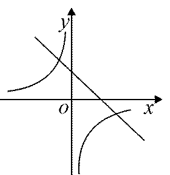 9. 二次函数 的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
9. 二次函数 的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )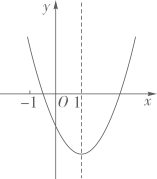 A、1 B、2个 C、3个 D、4个10. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= 上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3…Sn.则Sn可表示为( )
A、1 B、2个 C、3个 D、4个10. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= 上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3…Sn.则Sn可表示为( )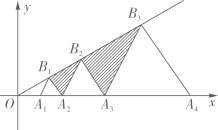 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题3分,共18分)
-
11. 因式分解:4ax2-4ax+a=.12. 若关于x、y的二元一次方程组 的解满足x+y≤0,则m的取值范围是.
 13. 一个圆锥的底面半径r=5,高h=10,则这个圆锥的侧面积是.14. 在平面直角坐标系中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为: ,则点P(3,-3)到直线 的距离为.15. 如图,已知线段AB=4,O是AB的中点,直线l经过点O,∠1=60°,P点是直线l上一点,当△APB为直角三角形时,则BP=.
13. 一个圆锥的底面半径r=5,高h=10,则这个圆锥的侧面积是.14. 在平面直角坐标系中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为: ,则点P(3,-3)到直线 的距离为.15. 如图,已知线段AB=4,O是AB的中点,直线l经过点O,∠1=60°,P点是直线l上一点,当△APB为直角三角形时,则BP=. 16. 如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=O B.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为.
16. 如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=O B.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为.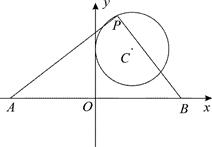
三、解答题(17~21题每题8分,22、23题每题10分,24题12分,共72分)
-
17. 先化简,再从-1、2、3、4中选一个合适的数作为x的值代入求值.18. 如图,矩形ABCD中,AB=8,AD=6,点O是对角线BD的中点,过点O的直线分别交AB、CD边于点E、F.
 (1)、求证:四边形DEBF是平行四边形;(2)、当DE=DF时,求EF的长.19. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.
(1)、求证:四边形DEBF是平行四边形;(2)、当DE=DF时,求EF的长.19. 某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中选出一类最喜爱的电视节目,以下是根据调查结果绘制的统计图表的一部分.类别
A
B
C
D
E
类型
新闻
体育
动画
娱乐
戏曲
人数
11
20
40
m
4
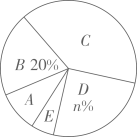
请你根据以上信息,回答下列问题:
(1)、统计表中m的值为 , 统计图中n的值为 , A类对应扇形的圆心角为度;(2)、该校共有1500名学生,根据调查结果,估计该校最喜爱体育节目的学生人数;(3)、样本数据中最喜爱戏曲节目的有4人,其中仅有1名男生.从这4人中任选2名同学去观赏戏曲表演,请用树状图或列表求所选2名同学中有男生的概率.20. 已知关于x的方程x2-2x+2k-1=0有实数根.(1)、求k的取值范围;(2)、设方程的两根分别是x1、x2 , 且 ,试求k的值.21. 为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度AB,他站在距离教学楼底部E处6米远的地面C处,测得宣传牌的底部B的仰角为60°,同时测得教学楼窗户D处的仰角为30°(A、B、D、E在同一直线上).然后,小明沿坡度i=1:1.5的斜坡从C走到F处,此时DF正好与地面CE平行. (1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米, ≈1.41, ≈1.73).22. 如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,P B.
(1)、求点F到直线CE的距离(结果保留根号);(2)、若小明在F处又测得宣传牌顶部A的仰角为45°,求宣传牌的高度AB(结果精确到0.1米, ≈1.41, ≈1.73).22. 如图,PA是⊙O的切线,切点为A,AC是⊙O的直径,连接OP交⊙O于E.过A点作AB⊥PO于点D,交⊙O于B,连接BC,P B.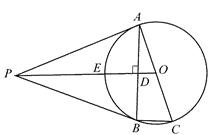 (1)、求证:PB是⊙O的切线;(2)、求证:E为△PAB的内心;(3)、若cos∠PAB= ,BC=1,求PO的长.23. “互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?24. 如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点,AB=4,交y轴于点C,对称轴是直线x=1.
(1)、求证:PB是⊙O的切线;(2)、求证:E为△PAB的内心;(3)、若cos∠PAB= ,BC=1,求PO的长.23. “互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?24. 如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点,AB=4,交y轴于点C,对称轴是直线x=1. (1)、求抛物线的解析式及点C的坐标;(2)、连接BC,E是线段OC上一点,E关于直线x=1的对称点F正好落在BC上,求点F的坐标;(3)、动点M从点O出发,以每秒2个单位长度的速度向点B运动,过M作x轴的垂线交抛物线于点N,交线段BC于点Q.设运动时间为t(t>0)秒.
(1)、求抛物线的解析式及点C的坐标;(2)、连接BC,E是线段OC上一点,E关于直线x=1的对称点F正好落在BC上,求点F的坐标;(3)、动点M从点O出发,以每秒2个单位长度的速度向点B运动,过M作x轴的垂线交抛物线于点N,交线段BC于点Q.设运动时间为t(t>0)秒.①若△AOC与△BMN相似,请直接写出t的值;
②△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.