2016-2017学年山东省日照市莒县八年级下学期期中数学试卷
试卷更新日期:2017-06-02 类型:期中考试
一、选择题
-
1. 用公式法解x2+3x=1时,先求出a、b、c的值,则a、b、c依次为( )A、1,3,1 B、1,3,﹣1 C、﹣1,﹣3,﹣1 D、﹣1,3,12. 某班10名学生的校服尺寸与对应人数如表所示:
尺寸(cm)
160
165
170
175
180
学生人数(人)
1
3
2
2
2
则这10名学生校服尺寸的众数和中位数分别为( )
A、165cm,165cm B、165cm,170cm C、170cm,165cm D、170cm,170cm3. 如果一个四边形的两条对角线互相平分且相等,那么它一定是( )A、矩形 B、菱形 C、正方形 D、梯形4. 用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )A、(x﹣2)2=2 B、(x+2)2=2 C、(x﹣2)2=﹣2 D、(x﹣2)2=65. 点P1(x1 , y1),点P2(x2 , y2)是一次函数y=﹣4x+3图象上的两个点,且x1<x2 , 则y1与y2的大小关系是( )A、y1>y2 B、y1>y2>0 C、y1<y2 D、y1=y26. 已知菱形的周长为40,一条对角线长为12,则这个菱形的面积为( )A、40 B、47 C、96 D、1907. 甲、乙两人各射靶5次,已知甲所中环数是8,7,9,7,9,乙所中环数的平均数, =8,方差 =0.4,那么,对甲、乙的射击成绩的正确判断是( )A、甲的射击成绩较稳定 B、乙的射击成绩较稳定 C、甲、乙的射击成绩同样稳定 D、甲、乙的射击成绩无法比较8. 根据如图的程序,计算当输入x=3时,输出的结果y是( ) A、2 B、4 C、6 D、89. 若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是( )A、
A、2 B、4 C、6 D、89. 若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是( )A、 B、
B、 C、
C、 D、
D、 10. 等腰三角形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( )A、8 B、10 C、8或10 D、不能确定11. 如图,直线y=kx+b经过点A(3,1)和点B(6,0),则不等式0<kx+b< x的解集为( )
10. 等腰三角形的底和腰是方程x2﹣6x+8=0的两根,则这个三角形的周长为( )A、8 B、10 C、8或10 D、不能确定11. 如图,直线y=kx+b经过点A(3,1)和点B(6,0),则不等式0<kx+b< x的解集为( ) A、x<0 B、0<x<3 C、3<x<6 D、x>612. 如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )
A、x<0 B、0<x<3 C、3<x<6 D、x>612. 如图,矩形ABCD的面积为20cm2 , 对角线交于点O;以AB、AO为邻边做平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边做平行四边形AO1C2B;…;依此类推,则平行四边形AO4C5B的面积为( )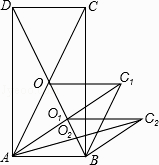 A、cm2 B、cm2 C、cm2 D、cm2
A、cm2 B、cm2 C、cm2 D、cm2二、填空题
-
13. 将直线y=2x+1向下平移3个单位长度后所得直线的解析式是14. 已知关于x的一元二次方程x2﹣2 x+1=0的实数根是x1、x2 , 则代数式x12+x22﹣x1x2 .15. 如图所示,矩形纸片ABCD中,AB=6cm,BC=8cm,现将其沿EF对折,使得点C与点A重合,则EF长为cm.
 16. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
16. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 . (把你认为正确说法的序号都填上)

三、解答题
-
17. 选用合适的方法解下列方程:(1)、2x2﹣5x=3;(2)、(x+3)2=(1﹣3x)2 .18. 某校教导处为了了解本校初二学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本校的初二学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示).请结合统计图中提供的信息,回答下列问题:
 (1)、本次所抽取样本的容量是多少?(2)、在被调查的学生中,一天做家庭作业所用的大致时间超过120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几?(3)、这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?19. 关于x的方程kx2+(k+2)x+ =0有两个不相等的实数根;(1)、求k的取值范围;(2)、是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,请说明理由.20. A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和10元;从B校调运一台电脑到C校和D校的运费分别为30元和20元.
(1)、本次所抽取样本的容量是多少?(2)、在被调查的学生中,一天做家庭作业所用的大致时间超过120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几?(3)、这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内?19. 关于x的方程kx2+(k+2)x+ =0有两个不相等的实数根;(1)、求k的取值范围;(2)、是否存在实数k,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,请说明理由.20. A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和10元;从B校调运一台电脑到C校和D校的运费分别为30元和20元. (1)、设A校运往C校的电脑为x台,请仿照下图,求总运费W(元)关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费是多少?21. 如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)、设A校运往C校的电脑为x台,请仿照下图,求总运费W(元)关于x的函数关系式;(2)、求出总运费最低的调运方案,最低运费是多少?21. 如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C. (1)、求直线l2的解析表达式;(2)、求△ADC的面积;(3)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标.22. 如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2 , 当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H.
(1)、求直线l2的解析表达式;(2)、求△ADC的面积;(3)、在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标.22. 如图1,矩形ABCD中,AB=7cm,AD=4cm,点E为AD上一定点,F为AD延长线上一点,且DF=acm,点P从A点出发,沿AB边向点B以2cm/s的速度运动,运动到B点停止,连结PE,设点P运动的时间为ts,△PAE的面积为ycm2 , 当0≤t≤1时,△PAE的面积y(cm2)关于时间t(s)的函数图象如图2所示,连结PF,交CD于点H. (1)、t的取值范围为 , AE=cm;(2)、如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?(3)、在(2)的条件下求出点P的运动时间t.
(1)、t的取值范围为 , AE=cm;(2)、如图3,将△HDF沿线段DF进行翻折,与CD的延长线交于点M,连结AM,当a为何值时,四边形PAMH为菱形?(3)、在(2)的条件下求出点P的运动时间t.