2016-2017学年山东省临沂市蒙阴县八年级下学期期中数学试卷

试卷更新日期：2017-06-02 类型：期中考试

进入出卷网下载

一、选择题

1. 二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是（）

A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
2. 下列根式中是最简二次根式的是（）

A、 $\sqrt{\frac{2}{3}}$ B、 $\sqrt{3}$ C、 $\sqrt{9}$ D、 $\sqrt{12}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{5}$ ﹣ $\sqrt{3}$ = $\sqrt{2}$ B、3 $\sqrt{5}$ ×2 $\sqrt{3}$ =6 $\sqrt{15}$ C、（2 $\sqrt{2}$ ）²=16 D、 $\frac{3}{\sqrt{3}}$ =1

查看试题解析
4. 如图，在Rt△ABC中，∠C=90°，∠B=30°，AB=8，则BC的长是（）

A、 $\frac{4 \sqrt{3}}{3}$ B、4 C、8 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
5. 如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为30海里的A处，轮船沿正南方向航行一段时间后，到达位于灯塔P的南偏东30°方向上的B处，则此时轮船所在位置B处与灯塔P之间的距离为（）

A、60海里 B、45海里 C、20 $\sqrt{3}$ 海里 D、30 $\sqrt{3}$ 海里

查看试题解析
6. 下列说法错误的是（）

A、对角线互相平分的四边形是平行四边形 B、两组对边分别相等的四边形是平行四边形 C、一组对边平行且相等的四边形是平行四边形 D、一组对边相等，另一组对边平行的四边形是平行四边形

查看试题解析
7. 已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（）

A、OE= $\frac{1}{2}$ DC B、OA=OC C、∠BOE=∠OBA D、∠OBE=∠OCE

查看试题解析
8. 如图，▱ABCD的对角线AC，BD交于点O，已知AD=8，BD=12，AC=6，则△OBC的周长为（）

A、13 B、17 C、20 D、26

查看试题解析
9. 平面直角坐标系中，已知▱ABCD的三个顶点坐标分别是A（m，n），B （ 2，﹣1 ），C（﹣m，﹣n），则点D的坐标是（）

A、（﹣2，1 ） B、（﹣2，﹣1 ） C、（﹣1，﹣2 ） D、（﹣1，2 ）

查看试题解析
10. 如图，矩形ABCD的对角线AC与BD相交于点O，CE∥BD，DE∥AC，AD=2 $\sqrt{3}$ ，DE=2，则四边形OCED的面积（）

A、2 $\sqrt{3}$ B、4 C、4 $\sqrt{3}$ D、8

查看试题解析
11. 如图，以直角三角形a、b、c为边，向外作等边三角形，半圆，等腰直角三角形和正方形，上述四种情况的面积关系满足S₁+S₂=S₃图形个数有（）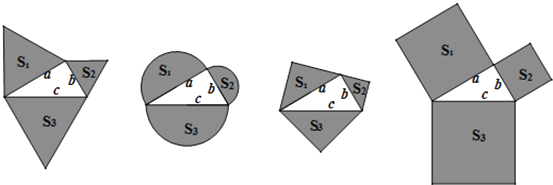

A、1 B、2 C、3 D、4

查看试题解析
12. 在△ABC中，AB=10，AC=2 $\sqrt{10}$ ，BC边上的高AD=6，则另一边BC等于（）

A、10 B、8 C、6或10 D、8或10

查看试题解析
13. 菱形ABCD的对角线AC，BD相交于点O，E，F分别是AD，CD边上的中点，连接EF．若EF= $\sqrt{2}$ ，BD=2，则菱形ABCD的面积为（）

A、2 $\sqrt{2}$ B、 $\sqrt{2}$ C、6 $\sqrt{2}$ D、8 $\sqrt{2}$

查看试题解析
14.
如图，已知菱形OABC的顶点O（0，0），B（2，2），若菱形绕点O逆时针旋转，每秒旋转45°，则第60秒时，菱形的对角线交点D的坐标为（）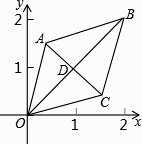

A、（1，﹣1） B、（﹣1，﹣1） C、（ $\sqrt{2}$ ，0） D、（0，﹣ $\sqrt{2}$ ）

查看试题解析

二、填空题

15. 直角三角形斜边长是5，一直角边的长是3，则此直角三角形的面积为．

查看试题解析
16. 计算2 $\sqrt{\frac{1}{2}}$ ﹣ $\sqrt{18}$ 的结果是．

查看试题解析
17. 代数式 $\frac{\sqrt{1 - x}}{x + 2}$ 有意义，则字母x的取值范围是．

查看试题解析
18. 如图在△ABC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB于点E，且BE=BF，请你添加一个条件，使四边形BECF是正方形．

查看试题解析
19.
如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…．若点A（ $\frac{3}{2}$ ，0），B（0，2），则点B₂₀₁₆的坐标为．

查看试题解析

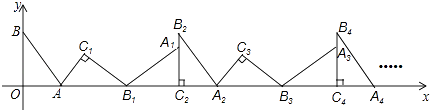
三、解答题

20. 计算下列各式：

(1)、 $\sqrt[3]{- 8}$ +（ $\frac{1}{3}$ ）^﹣²+（π﹣1）⁰

(2)、（3﹣π）⁰+4× $\sqrt{\frac{1}{2}}$ ﹣ $\sqrt{8}$ +|1﹣ $\sqrt{3}$ |．

查看试题解析
21. 观察下列等式：
第1个等式：a₁= $\frac{1}{1 + \sqrt{2}}$ = $\sqrt{2}$ ﹣1；第2个等式：a₂= $\frac{1}{\sqrt{2} + \sqrt{3}}$ = $\sqrt{3}$ ﹣ $\sqrt{2}$ ；
第3个等式：a₃= $\frac{1}{\sqrt{3} + 2}$ =2﹣ $\sqrt{3}$ ；第4个等式：a₄= $\frac{1}{2 + \sqrt{5}}$ = $\sqrt{5}$ ﹣2；
…
按上述规律，回答以下问题：

(1)、请写出第n个等式：a_n=；

(2)、求a₁+a₂+a₃+…+a_n的值．

查看试题解析
22. 在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．
某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．
作AD⊥BC于D，设BD=x，用含x的代数式表示CD→根据勾股定理，利用AD作为“桥梁”，建立方程模型求出x→利用勾股定理求出AD的长，再计算三角形的面积．

查看试题解析
23. 如图，已知BD是矩形ABCD的对角线．

(1)、用直尺和圆规作线段BD的垂直平分线，分别交AD、BC于E、F（保留作图痕迹，不写作法和证明）．

(2)、连结BE，DF，问四边形BEDF是什么四边形？请说明理由．

查看试题解析
24. 定义：如图1，点M，N把线段AB分割成AM，MN和BN，若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．
请解决下列问题：

(1)、已知点M，N是线段AB的勾股分割点，且BN＞MN＞AM．若AM=2，MN=3，求BN的长；

(2)、如图2，若点F、M、N、G分别是AB、AD、AE、AC边上的中点，点D，E是线段BC的勾股分割点，且EC＞DE＞BD，求证：点M，N是线段FG的勾股分割点．

查看试题解析