四川省南充市2019年中考数学试卷
试卷更新日期:2019-06-26 类型:中考真卷
一、单选题
-
1. 如果 ,那么 的值为( )A、6 B、 C、-6 D、2. 下列各式计算正确的是( )A、x+x2=x3 B、 C、 D、3. 如图是一个几何体的表面展开图,这个几何体是( )
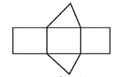 A、
A、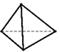 B、
B、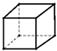 C、
C、 D、
D、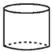 4. 在2019年南充市初中毕业升学体育与健康考试中,某校九年级(1)班体育委员对本班50名同学参加球类自选项目做了统计,制作出扇形统计图(如图),则该班选考乒乓球人数比羽毛球人数多( )
4. 在2019年南充市初中毕业升学体育与健康考试中,某校九年级(1)班体育委员对本班50名同学参加球类自选项目做了统计,制作出扇形统计图(如图),则该班选考乒乓球人数比羽毛球人数多( )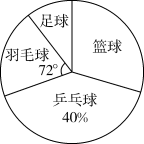 A、5人 B、10人 C、15人 D、20人5. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )
A、5人 B、10人 C、15人 D、20人5. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,若BC=6,AC=5,则△ACE的周长为( )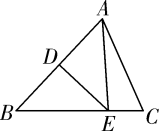 A、8 B、11 C、16 D、176. 关于 的一元一次方程 的解为 ,则 的值为( )A、9 B、8 C、5 D、47. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A、8 B、11 C、16 D、176. 关于 的一元一次方程 的解为 ,则 的值为( )A、9 B、8 C、5 D、47. 如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )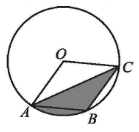 A、6π B、 π C、 π D、2π8. 关于 的不等式 只有2个正整数解,则 的取值范围为( )A、 B、 C、 D、9. 抛物线 ( 是常数), ,顶点坐标为 .给出下列结论:①若点 与点 在该抛物线上,当 时,则 ;②关于 的一元二次方程 无实数解,那么( )A、①正确,②正确 B、①正确,②错误 C、①错误,②正确 D、①错误,②错误
A、6π B、 π C、 π D、2π8. 关于 的不等式 只有2个正整数解,则 的取值范围为( )A、 B、 C、 D、9. 抛物线 ( 是常数), ,顶点坐标为 .给出下列结论:①若点 与点 在该抛物线上,当 时,则 ;②关于 的一元二次方程 无实数解,那么( )A、①正确,②正确 B、①正确,②错误 C、①错误,②正确 D、①错误,②错误二、填空题
-
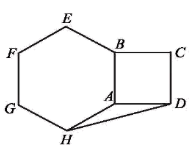
10. 原价为 元的书包,现按8折出售,则售价为元.11. 如图,以正方形ABCD的AB边向外作正六边形ABEFGH,连接DH,则∠ADH=°
 12. 计算: + = .13. 下表是某养殖户的500只鸡出售时质量的统计数据.
12. 计算: + = .13. 下表是某养殖户的500只鸡出售时质量的统计数据.质量/kg
1.0
1.2
1.4
1.6
1.8
2.0
频数/只
56
162
112
120
40
10
则500只鸡质量的中位数为.
14. 在平面直角坐标系 中,点 在直线 上,点 在双曲线 上,则 的取值范围为.15. 如图,矩形硬纸片ABCD的顶点A在 轴的正半轴及原点上滑动,顶点B在 轴的正半轴及原点上滑动,点E为AB的中点,AB=24,BC=5,给出下列结论:①点A从点O出发,到点B运动至点O为止,点E经过的路径长为12π;②△OAB的面积的最大值为144;③当OD最大时,点D的坐标为 ,其中正确的结论是(填写序号).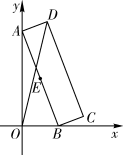
三、解答题
-
16. 计算:17. 如图,点O是线段AB的中点,OD∥BC且OD=BC.
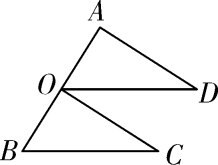 (1)、求证:△AOD≌△OBC;(2)、若∠ADO=35°,求∠DOC的度数.18. 现有四张完全相同的不透明卡片,其正面分别写有数字-2,-1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.(1)、随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;(2)、先随机抽取卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.19. 已知关于 的一元二次方程 有实数根.(1)、求实数m的取值范围;(2)、当m=2时,方程的根为 ,求代数式 的值.20. 双曲线 (k为常数,且 )与直线 交于 两点.
(1)、求证:△AOD≌△OBC;(2)、若∠ADO=35°,求∠DOC的度数.18. 现有四张完全相同的不透明卡片,其正面分别写有数字-2,-1,0,2,把这四张卡片背面朝上洗匀后放在桌面上.(1)、随机抽取一张卡片,求抽取的卡片上的数字为负数的概率;(2)、先随机抽取卡片,其上的数字作为点A的横坐标;然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线y=2x上的概率.19. 已知关于 的一元二次方程 有实数根.(1)、求实数m的取值范围;(2)、当m=2时,方程的根为 ,求代数式 的值.20. 双曲线 (k为常数,且 )与直线 交于 两点.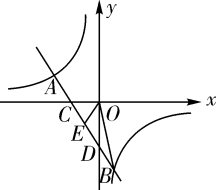 (1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.21. 如图,在△ABC中,以AC为直径的⊙O交AB于点D,连接CD,∠BCD=∠A.
(1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.21. 如图,在△ABC中,以AC为直径的⊙O交AB于点D,连接CD,∠BCD=∠A. (1)、求证:BC是⊙O的切线;(2)、若BC=5,BD=3,求点O到CD的距离.22. 在“我为祖国点赞”征文活动中,学校计划对获得一、二等奖的学生分别奖励一支钢笔,一本笔记本.已知购买2支钢笔和3个笔记本共38元,购买4支钢笔和5个笔记本共70元.(1)、钢笔、笔记本的单价分别为多少元?(2)、经与商家协商,购买钢笔超过30支时,每增加一支,单价降低0.1元;超过50支,均按购买50支的单价销售.笔记本一律按原价销售.学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过60人,这次奖励一等学生多少人时,购买奖品金额最少,最少为多少元?23. 如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.
(1)、求证:BC是⊙O的切线;(2)、若BC=5,BD=3,求点O到CD的距离.22. 在“我为祖国点赞”征文活动中,学校计划对获得一、二等奖的学生分别奖励一支钢笔,一本笔记本.已知购买2支钢笔和3个笔记本共38元,购买4支钢笔和5个笔记本共70元.(1)、钢笔、笔记本的单价分别为多少元?(2)、经与商家协商,购买钢笔超过30支时,每增加一支,单价降低0.1元;超过50支,均按购买50支的单价销售.笔记本一律按原价销售.学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过60人,这次奖励一等学生多少人时,购买奖品金额最少,最少为多少元?23. 如图,在正方形ABCD中,点E是AB边上的一点,以DE为边作正方形DEFG,DF与BC交于点M,延长EM交GF于点H,EF与GB交于点N,连接CG.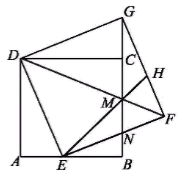 (1)、求证:CD⊥CG;(2)、若tan∠MEN= ,求 的值;(3)、已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为 ?请说明理由.24. 如图,抛物线 与 轴交于点A(-1,0),点B(-3,0),且OB=OC,
(1)、求证:CD⊥CG;(2)、若tan∠MEN= ,求 的值;(3)、已知正方形ABCD的边长为1,点E在运动过程中,EM的长能否为 ?请说明理由.24. 如图,抛物线 与 轴交于点A(-1,0),点B(-3,0),且OB=OC,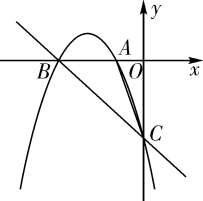 (1)、求抛物线的解析式;(2)、点P在抛物线上,且∠POB=∠ACB,求点P的坐标;(3)、抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.
(1)、求抛物线的解析式;(2)、点P在抛物线上,且∠POB=∠ACB,求点P的坐标;(3)、抛物线上两点M,N,点M的横坐标为m,点N的横坐标为m+4.点D是抛物线上M,N之间的动点,过点D作y轴的平行线交MN于点E.①求DE的最大值.
②点D关于点E的对称点为F.当m为何值时,四边形MDNF为矩形?