山东省滨州市2019年中考数学试卷
试卷更新日期:2019-06-26 类型:中考真卷
一、单选题
-
1. 下列各数中,负数是( ).A、 B、 C、 D、2. 下列计算正确的是( ).A、 B、 C、 D、3. 如图, , , 平分 ,则 的度数等于( ).
 A、26° B、52° C、54° D、77°4. 如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列说法正确的是( ).
A、26° B、52° C、54° D、77°4. 如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列说法正确的是( ).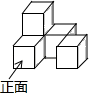 A、主视图的面积为4 B、左视图的面积为4 C、俯视图的面积为3 D、三种视图的面积都是45. 在平面直角坐标系中,将点 向上平移3个单位长度,再向左平移2个单位长度,得到点 ,则点 的坐标是( ).A、 B、 C、 D、6. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).
A、主视图的面积为4 B、左视图的面积为4 C、俯视图的面积为3 D、三种视图的面积都是45. 在平面直角坐标系中,将点 向上平移3个单位长度,再向左平移2个单位长度,得到点 ,则点 的坐标是( ).A、 B、 C、 D、6. 如图, 为 的直径, 为 上两点,若 ,则 的大小为( ).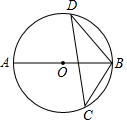 A、60° B、50° C、40° D、20°7. 若 与 的和是单项式,则 的平方根为( ).A、4 B、8 C、±4 D、±88. 用配方法解一元二次方程 时,下列变形正确的是( ).A、 B、 C、 D、9. 已知点 关于原点对称的点在第四象限,则 的取值范围在数轴上表示正确的是( ).A、
A、60° B、50° C、40° D、20°7. 若 与 的和是单项式,则 的平方根为( ).A、4 B、8 C、±4 D、±88. 用配方法解一元二次方程 时,下列变形正确的是( ).A、 B、 C、 D、9. 已知点 关于原点对称的点在第四象限,则 的取值范围在数轴上表示正确的是( ).A、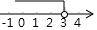 B、
B、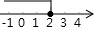 C、
C、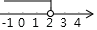 D、
D、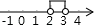 10. 满足下列条件时, 不是直角三角形的为( ).A、 B、 C、 D、11. 如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中正确的个数为( ).
10. 满足下列条件时, 不是直角三角形的为( ).A、 B、 C、 D、11. 如图,在 和 中, ,连接 交于点 ,连接 .下列结论:① ;② ;③ 平分 ;④ 平分 .其中正确的个数为( ). A、4 B、3 C、2 D、112. 如图,在平面直角坐标系中,菱形 的边 在 轴的正半轴上,反比例函数 的图象经过对角线 的中点 和顶点 .若菱形 的面积为12,则 的值为( ).
A、4 B、3 C、2 D、112. 如图,在平面直角坐标系中,菱形 的边 在 轴的正半轴上,反比例函数 的图象经过对角线 的中点 和顶点 .若菱形 的面积为12,则 的值为( ).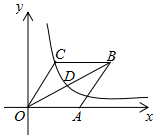 A、6 B、5 C、4 D、3
A、6 B、5 C、4 D、3二、填空题
-
13. 计算: .14. 方程 的解是 .15. 若一组数据 的平均数为6,众数为5,则这组数据的方差为 .16. 在平面直角坐标系中, 三个顶点的坐标分别为 .以原点 为位似中心,把这个三角形缩小为原来的 ,得到 ,则点 的对应点 的坐标是 .17. 若正六边形的内切圆半径为2,则其外接圆半径为 .18. 如图,直线 经过点 ,当 时, 的取值范围为 .
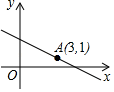 19. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号)
19. 如图, 的对角线 交于点 , 平分 交 于点 ,交 于点 ,且 ,连接 .下列结论:① ;② ;③ ;④ .其中正确的结论有(填写所有正确结论的序号) 20. 观察下列一组数:
20. 观察下列一组数:,
它们是按一定规律排列的,请利用其中规律,写出第 个数 (用含 的式子表示)
三、解答题
-
21. 先化简,再求值: ,其中 是不等式组 的整数解.22. 有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.(1)、请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?(2)、某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.23. 某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)、两个班共有女生多少人?(2)、将频数分布直方图补充完整;(3)、求扇形统计图中 部分所对应的扇形圆心角度数;(4)、身高在 的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.24. 如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 .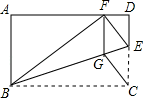 (1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.
(1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.