山东省济宁市2019年中考数学试卷
试卷更新日期:2019-06-26 类型:中考模拟
一、单选题
-
1. 下列四个实数中,最小的是( )A、 B、-5 C、1 D、42. 如图,直线 , 被直线 , 所截,若 , ,则 的度数是( )
 A、65° B、60° C、55° D、75°3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
A、65° B、60° C、55° D、75°3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、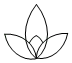 D、
D、 4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量5. 下列计算正确的是( )A、 B、 C、 D、6. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、7. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )
4. 以下调查中,适宜全面调查的是( )A、调查某批次汽车的抗撞击能力 B、调查某班学生的身高情况 C、调查春节联欢晚会的收视率 D、调查济宁市居民日平均用水量5. 下列计算正确的是( )A、 B、 C、 D、6. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、7. 如图,一个几何体上半部为正四棱锥,下半部为立方体,且有一个面涂有颜色,该几何体的表面展开图是( )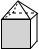 A、
A、 B、
B、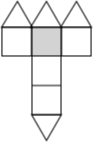 C、
C、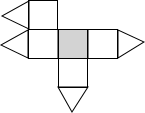 D、
D、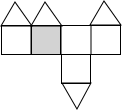 8. 将抛物线 向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A、 B、 C、 D、9. 如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到 .若反比例函数 的图象恰好经过 的中点D,则k的值是( )
8. 将抛物线 向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A、 B、 C、 D、9. 如图,点A的坐标是(-2,0),点B的坐标是(0,6),C为OB的中点,将△ABC绕点B逆时针旋转90°后得到 .若反比例函数 的图象恰好经过 的中点D,则k的值是( )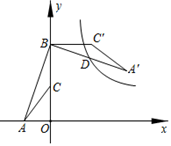 A、9 B、12 C、15 D、1810. 已知有理数 ,我们把 称为a的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数……依此类推,那么 的值是( )A、-7.5 B、7.5 C、5.5 D、-5.5
A、9 B、12 C、15 D、1810. 已知有理数 ,我们把 称为a的差倒数,如:2的差倒数是 ,-1的差倒数是 .如果 ,a2是a1的差倒数,a3是a2的差倒数,a4是a3的差倒数……依此类推,那么 的值是( )A、-7.5 B、7.5 C、5.5 D、-5.5二、填空题
-
11. 已知x=1是方程x2+bx﹣2=0的一个根,则方程的另一个根是 .12. 如图,该硬币边缘镌刻的正九边形每个内角的度数是 .
 13. 已知点 位于第二象限,并且 , 为整数,写出一个符合上述条件的点 的坐标: .14. 如图,O为Rt△ABC直角边AC上一点,以OC为半径的 ⊙O与斜边AB相切于点D,交OA于点E,已知BC= ,AC=3.则图中阴影部分的面积是 .
13. 已知点 位于第二象限,并且 , 为整数,写出一个符合上述条件的点 的坐标: .14. 如图,O为Rt△ABC直角边AC上一点,以OC为半径的 ⊙O与斜边AB相切于点D,交OA于点E,已知BC= ,AC=3.则图中阴影部分的面积是 . 15. 如图,抛物线 与直线 交于A(-1,P),B(3,q)两点,则不等式 的解集是 .
15. 如图,抛物线 与直线 交于A(-1,P),B(3,q)两点,则不等式 的解集是 .
三、解答题
-
16. 计算:17. 某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 (小时)
人数
占女生人数百分比
4
5
6
2

根据图表解答下列问题:
(1)、在女生阅读时间人数统计表中, , ;(2)、此次抽样调查中,共抽取了名学生,学生阅读时间的中位数在时间段;(3)、从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?18. 如图,点 和点 在 内部.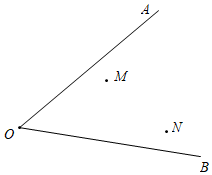 (1)、请你作出点 ,使点 到点 和点 的距离相等,且到 两边的距离也相等(保留作图痕迹,不写作法);(2)、请说明作图理由.19. 小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离 与小王的行驶时间 之间的函数关系.
(1)、请你作出点 ,使点 到点 和点 的距离相等,且到 两边的距离也相等(保留作图痕迹,不写作法);(2)、请说明作图理由.19. 小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离 与小王的行驶时间 之间的函数关系.请你根据图象进行探究:
 (1)、小王和小李的速度分别是多少?(2)、求线段 所表示的 与 之间的函数解析式,并写出自变量 的取值范围.20. 如图, 是 的直径, 是 上一点, 是 的中点, 为 延长线上一点,且 , 与 交于点 ,与 交于点 .
(1)、小王和小李的速度分别是多少?(2)、求线段 所表示的 与 之间的函数解析式,并写出自变量 的取值范围.20. 如图, 是 的直径, 是 上一点, 是 的中点, 为 延长线上一点,且 , 与 交于点 ,与 交于点 . (1)、求证: 是 的切线;(2)、若 , ,求直径 的长.21. 阅读下面的材料:
(1)、求证: 是 的切线;(2)、若 , ,求直径 的长.21. 阅读下面的材料:如果函数 满足:对于自变量 的取值范围内的任意 , ,
①若 ,都有 ,则称 是增函数;
②若 ,都有 ,则称 是减函数.
例题:证明函数 是减函数.
证明:设 ,
.
∵ ,
∴ , .
∴ .即 .
∴ .
∴函数 是减函数.
根据以上材料,解答下面的问题:
已知函数 ,
,
(1)、计算: , ;(2)、猜想:函数 是函数(填“增”或“减”);(3)、请仿照例题证明你的猜想.22. 如图1,在矩形 中, , , 是 边上一点,连接 ,将矩形 沿 折叠,顶点 恰好落在 边上点 处,延长 交 的延长线于点 . (1)、求线段 的长;(2)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 ,设 , .
(1)、求线段 的长;(2)、如图2, , 分别是线段 , 上的动点(与端点不重合),且 ,设 , .①写出 关于 的函数解析式,并求出 的最小值;
②是否存在这样的点 ,使 是等腰三角形?若存在,请求出 的值;若不存在,请说明理由.