浙江省舟山市2019年中考数学试卷
试卷更新日期:2019-06-25 类型:中考真卷
一、选择题
-
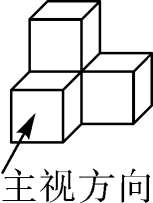
1. 的相反数是( )A、2019 B、-2019 C、 D、-2. 年 月 日 时 分,“嫦娥四号”探测器飞行约 千米,实现人类探测器首次在月球背面软着陆.数据 用科学记数法表示为( )A、 B、 C、 D、3. 如图是由四个相同的小正方形组成的立体图形,它的俯视图为( )
 A、
A、 B、
B、 C、
C、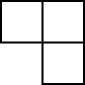 D、
D、 4. 年 月 日第 届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )
4. 年 月 日第 届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )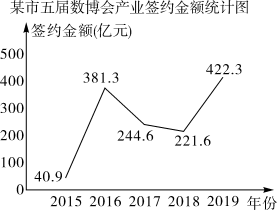 A、 签约金额逐年增加 B、与上年相比,2019年的签约金额的增长量最多 C、签约金额的年增长速度最快的是2016年 D、2018年的签约金额比2017年降低了22.98%5. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则 可以是( )
A、 签约金额逐年增加 B、与上年相比,2019年的签约金额的增长量最多 C、签约金额的年增长速度最快的是2016年 D、2018年的签约金额比2017年降低了22.98%5. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则 可以是( )20
a
A、 B、-1 C、0 D、6. 已知四个实数 , , , ,若 , ,则( )A、 B、 C、 D、7. 如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA的长为( )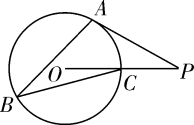 A、2 B、 C、 D、8. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为( )A、 B、 C、 D、9. 如图,在直角坐标系中,已知菱形 的顶点 , .作菱形 关于 轴的对称图形 ,再作图形 关于点 的中心对称图形 ,则点 的对应点 的坐标是( )
A、2 B、 C、 D、8. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 两,牛每头 两,根据题意可列方程组为( )A、 B、 C、 D、9. 如图,在直角坐标系中,已知菱形 的顶点 , .作菱形 关于 轴的对称图形 ,再作图形 关于点 的中心对称图形 ,则点 的对应点 的坐标是( )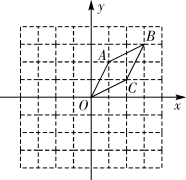 A、 B、 C、 D、10. 小飞研究二次函数 ( 为常数)性质时如下结论:
A、 B、 C、 D、10. 小飞研究二次函数 ( 为常数)性质时如下结论:①这个函数图象的顶点始终在直线 上;②存在一个 的值,使得函数图象的顶点与 轴的两个交点构成等腰直角三角形;③点 与点 在函数图象上,若 , ,则 ;④当 时, 随 的增大而增大,则 的取值范围为 其中错误结论的序号是( )
A、① B、② C、③ D、④二、填空题
-
11. 分解因式: = .
12. 从甲、乙、丙三人中任选两人参加“青年志愿者”活动,甲被选中的概率为 .13. 数轴上有两个实数 , ,且 >0, <0, + <0,则四个数 , , , 的大小关系为(用“<”号连接).14. 在x2+ +4=0的括号中添加一个关于x的一次项,使方程有两个相等的实数根。
15. 如图,在△ABC中,若∠A=45°,AC2-BC2= AB2 , 则tanC=。 16. 如图,一副含30°和45°角的三角板 和 拼合在个平面上,边 与 重合, .当点 从点 出发沿 方向滑动时,点 同时从点 出发沿射线 方向滑动.当点 从点 滑动到点 时,点 运动的路径长为 ;连接 ,则△ 的面积最大值为 .
16. 如图,一副含30°和45°角的三角板 和 拼合在个平面上,边 与 重合, .当点 从点 出发沿 方向滑动时,点 同时从点 出发沿射线 方向滑动.当点 从点 滑动到点 时,点 运动的路径长为 ;连接 ,则△ 的面积最大值为 .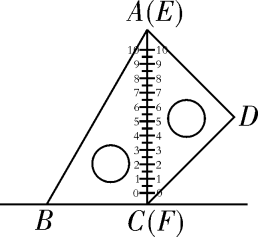
三、解答题
-
17. 小明解答“先化简,再求值: ,其中
.”的过程如图.请指出解答过程中错误
步骤的序号,并写出正确的解答过程.
 18. 如图,在矩形 ABCD中,点 E,F 在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明.
18. 如图,在矩形 ABCD中,点 E,F 在对角线BD.请添加一个条件,使得结论“AE=CF”成立,并加以证明. 19. 如图,在直角坐标系中,已知点 (4,0),等边三角形 的顶点 在反比例函数 的图象上
19. 如图,在直角坐标系中,已知点 (4,0),等边三角形 的顶点 在反比例函数 的图象上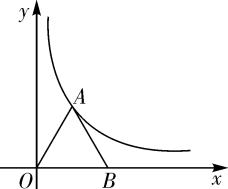 (1)、求反比例函数的表达式.(2)、把△ 向右平移 个单位长度,对应得到△ ,当这个函数图象经过△ 一边的中点时,求 的值.
(1)、求反比例函数的表达式.(2)、把△ 向右平移 个单位长度,对应得到△ ,当这个函数图象经过△ 一边的中点时,求 的值.
20. 在 6×6 的方格纸中,点 A,B,C 都在格点上,按要求画图: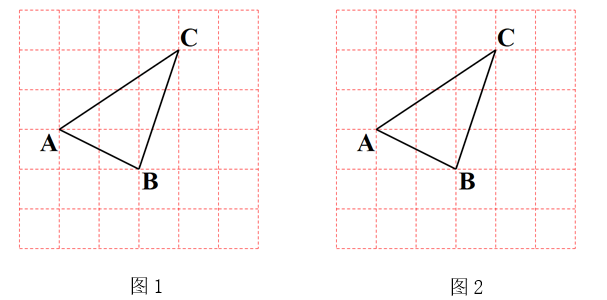 (1)、在图1中找一个格点D,使以点 A,B,C,D 为顶点的四边形是平行四边形.(2)、在图2中仅用无刻度的直尺,把线段AB 三等分(保留画图痕迹,不写画法).21. 在“创全国文明城市”活动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A、B 两小区分别有 500 名居民参加了测试,社区从中各随机抽取50 名居民成绩进行整理得到部分信息:
(1)、在图1中找一个格点D,使以点 A,B,C,D 为顶点的四边形是平行四边形.(2)、在图2中仅用无刻度的直尺,把线段AB 三等分(保留画图痕迹,不写画法).21. 在“创全国文明城市”活动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A、B 两小区分别有 500 名居民参加了测试,社区从中各随机抽取50 名居民成绩进行整理得到部分信息:【信息一】A 小区 50 名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值):
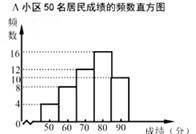
【信息二】上图中,从左往右
第四组的成绩如下

【信息三】A、B 两小区各 50 名居民成绩的平均数、中位数、众数、优秀率(80 分及以上为优秀)、方差等数据如下(部分空缺):

根据以上信息,回答下列问题:
(1)、求A小区50名居民成绩的中位数.(2)、请估计A小区500名居民成绩能超过平均数的人数.(3)、请尽量从多个角度,选择合适的统计量分析 A,B 两小区参加测试的居民掌握垃圾分类知识的情况.22. 某挖掘机的底座高 米,动臂 米, 米, 与 的固定夹角∠ =140°.初始位置如图1,斗杆顶点 与铲斗顶点 所在直线 垂直地面 于点 ,测得∠ =70°(示意图2).工作时如图3,动臂 会绕点 转动,当点 , , 在同一直线时,斗杆顶点 升至最高点(示意图4).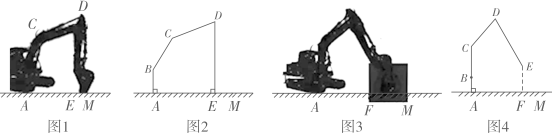
(考数据: , , , , )(1)、求挖掘机在初始位置时动臂 与 的夹角∠ 的度数.(2)、问斗杆顶点 的最高点比初始位置高了多少米(精确到0.1米)?
23. 某农作物的生长率 与温度 ( )有如下关系:如图,当10≤ ≤25 时可近似用函数 刻画;当25≤ ≤37 时可近似用函数 刻画.
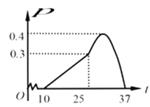 (1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系,部分数据如下:
(1)、求 的值.(2)、按照经验,该作物提前上市的天数 (天)与生长率 满足函数关系,部分数据如下:生长率
0.2
0.25
0.3
0.35
提前上市的天数 (天)
0
5
10
15
求:①求 关于 的函数表达式;
②请用含 的代数式表示
③天气寒冷,大棚加温可改变农作物生长速度.在大棚恒温20℃时每天的成本为100元,该作物30天后上市时,根据市场调查:每提前一天上市售出(一次售完),销售额可增加600元.因此决定给大棚继续加温,但加温导致成本增加,估测加温到20≤t≤25时的成本为200元/天,但若加温到25<t≤37,由于要采用特殊方法,成本增加到400元/天,问加温到多少度时增加的利润最大?并说明理由。(注:农作物上市售出后大鹏暂停使用)
24. 小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.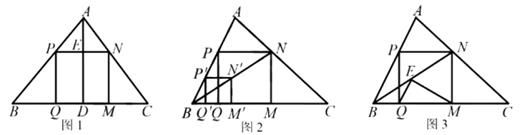
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
(1)、温故:如图1,在△ 中, ⊥ 于点 ,正方形 的边 在 上,顶点 , 分别在 , 上,若 BC=a,AD=h,求正方形 的边长(a,h表示).(2)、操作:如何能画出这个正方形PQMN呢?如图2,小波画出了图1的△ABC,然后按数学家波利亚在《怎样解题》中的方法进行操作,先在AB上任取一点 ,画正方形 ,使 , 在 边上, 在△ 内,然后连结 并延长交 于点N,画 ⊥ 于点 , ⊥ 交 于点 , ⊥ 于点 ,得到四边形P .
推理:证明图2中的四边形 是正方形.
(3)、拓展:小波把图2中的线段BN称为“波利亚线”,在该线截取 ,连结 , (如图3).当∠ =90°时,求“波利亚线”BN的长(用a、h表示).