辽宁省大连市甘井子区2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2019-06-25 类型:期中考试
一、单选题
-
1. 的立方根是( )A、 B、 C、 D、2. 点 的位置在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列实数中,属于无理数的是( )A、 B、 C、 D、4. 下列各组数中,属于方程 的解是( )A、 B、 C、 D、5. 在平面直角坐标系中,将点P(3,2)向右平移2个单位长度,再向下平移2个单位长度,所得到的点坐标为( )A、(1,0) B、(1,2) C、(5,4) D、(5,0)6. 对于二元一次方程 用含 的式子表示 为( )A、 B、 C、 D、7. 如图,∠1=65°,CD∥EB,则∠B的度数为( )
 A、65° B、110° C、105° D、115°8. 下列说法正确的是( )A、同位角相等 B、相等的角是对顶角 C、垂线段最短 D、两直线平行,同旁内角相等9. 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
A、65° B、110° C、105° D、115°8. 下列说法正确的是( )A、同位角相等 B、相等的角是对顶角 C、垂线段最短 D、两直线平行,同旁内角相等9. 如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )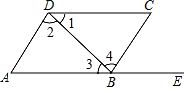 A、∠1=∠3 B、∠2=∠4 C、∠C=∠CBE D、∠C+∠ABC=180°10. 若线段AB∥x轴且AB=3,点A的坐标为(2,1),则点B的坐标为( )A、(5,1) B、(﹣1,1) C、(5,1)或(﹣1,1) D、(2,4)或(2,﹣2)
A、∠1=∠3 B、∠2=∠4 C、∠C=∠CBE D、∠C+∠ABC=180°10. 若线段AB∥x轴且AB=3,点A的坐标为(2,1),则点B的坐标为( )A、(5,1) B、(﹣1,1) C、(5,1)或(﹣1,1) D、(2,4)或(2,﹣2)二、填空题
-
11. 计算: .12. 计算: .13. 比较大小: 填“ ”、“ ”或“ ” .14. 如图,AO⊥CO,BO⊥DO,∠AOD=150°,则∠BOC的度数是.
 15. 如图是一个围棋棋盘的局部,若把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-2),白棋③的坐标是(-1,-4),则黑棋②的坐标是 .
15. 如图是一个围棋棋盘的局部,若把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-2),白棋③的坐标是(-1,-4),则黑棋②的坐标是 .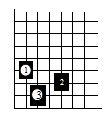 16. 如图所示平面直角坐标系中,四边形ABCD是边长为1的正方形,以A为圆心,AC为半径画圆交x轴负半轴于点P,则点P的坐标为.
16. 如图所示平面直角坐标系中,四边形ABCD是边长为1的正方形,以A为圆心,AC为半径画圆交x轴负半轴于点P,则点P的坐标为.
三、解答题
-
17. 解下列方程组:(1)、(2)、18. 已知一个正数的两个不相等的平方根是 与 .(1)、求 的值;(2)、求关于 的方程 的解19. 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,∠AOD=50°,求∠DOP的度数.
 20. 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点 的坐标是(-2,2),现将△ABC平移,使点A对应点为点 点 分别是B、C的对应点.
20. 在平面直角坐标系中,△ABC的三个顶点的位置如图所示,点 的坐标是(-2,2),现将△ABC平移,使点A对应点为点 点 分别是B、C的对应点. (1)、请画出平移后的 (不写画法);(2)、直接写出点 的坐标;(3)、若△ABC内部一点P的坐标为 则点P的对应点 的坐标是.21. 已知 是方程组 的解,求 的平方根。22. 某饮料加工厂生产的A、B两种饮料均需加入同种派加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产多少瓶?23. 如图,∠1+∠2=180°,∠3=∠B,求证:EF∥BC.
(1)、请画出平移后的 (不写画法);(2)、直接写出点 的坐标;(3)、若△ABC内部一点P的坐标为 则点P的对应点 的坐标是.21. 已知 是方程组 的解,求 的平方根。22. 某饮料加工厂生产的A、B两种饮料均需加入同种派加剂,A饮料每瓶需加该添加剂2克,B饮料每瓶需加该添加剂3克,已知270克该添加剂恰好生产了A、B两种饮料共100瓶,问A、B两种饮料各生产多少瓶?23. 如图,∠1+∠2=180°,∠3=∠B,求证:EF∥BC.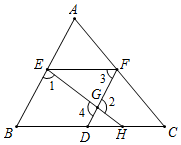 24. 如图,平面直角坐标系中,点A(0,3)、B(-2,0)、C(1,-1),连接AB、BC、AC.
24. 如图,平面直角坐标系中,点A(0,3)、B(-2,0)、C(1,-1),连接AB、BC、AC. (1)、求△ABC面积;(2)、点P为 轴上一动点,当 时,求点P的坐标。25. (问题发现)
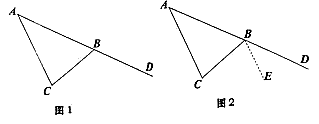
(1)、求△ABC面积;(2)、点P为 轴上一动点,当 时,求点P的坐标。25. (问题发现)如图1,D是△ABC边AB延长线上一点,求证:∠A+∠C=∠CBD.
小白同学的想法是,过点B作BE∥AC,从而将∠A和∠C转移到∠CBD处,使这三个角有公共顶点B,请你按照小白的想法,完成解答;
(问题解决)
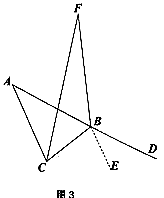
在上述问题的前提,如图3,从点B引一条射线与∠ACB的角平分线交于点F,且∠CBF=∠DBF,探究∠A与∠F的数量关系。在小白想法的提示下,小黑同学也想通过作平行线将∠A或∠F的位置进行转移,使两角有公共顶点,请你根据小黑的想法或者学过的知识解决此问题。
 26. 如图,正方形OABC边长为20,点D的坐标为( ,0),且 以OD、DE为邻边作长方形ODEF.
26. 如图,正方形OABC边长为20,点D的坐标为( ,0),且 以OD、DE为邻边作长方形ODEF. (1)、请直接写出以下点的坐标:E , F(用含 的式子表示);(2)、设长方形ODEF与正方形OABC重叠部分面积为S,求S(用含 的式子表示);(3)、S的值能否等于300,若能请求出此时 的值;若不能,请说明理由。
(1)、请直接写出以下点的坐标:E , F(用含 的式子表示);(2)、设长方形ODEF与正方形OABC重叠部分面积为S,求S(用含 的式子表示);(3)、S的值能否等于300,若能请求出此时 的值;若不能,请说明理由。