江苏省宜兴市张渚徐舍教学联盟2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2019-06-25 类型:期中考试
一、单选题
-
1. 在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列等式从左到右的变形中,属于因式分解的是( )A、x2-6x=x(x-6) B、(x+3)2=x2+6x+9 C、x2-4+4x=(x+2)(x-2)+4x D、8a2b4=2ab2·4ab23. 下列等式正确的是( )A、a4+a5=a9 B、a3•a3•a3=3a3 C、2a4•3a5=6a9 D、(﹣a3)4=a74. 下列各组线段不能组成三角形的是( )A、4cm、4cm、5cm B、4cm、6cm、11cm C、4cm、5cm、6cm D、5cm、12cm、13cm5. 若a=0.32 , b=﹣3﹣2 , c=(﹣3)0 , 那么a、b、c三数的大小为( )A、a>c>b B、a>b>c C、c>b>a D、c>a>b6. 一个多边形的内角和是900°,则这个多边形的边数为 ( )A、6 B、7 C、8 D、97. 下列图形中,由 ,能得到 的是( )A、
2. 下列等式从左到右的变形中,属于因式分解的是( )A、x2-6x=x(x-6) B、(x+3)2=x2+6x+9 C、x2-4+4x=(x+2)(x-2)+4x D、8a2b4=2ab2·4ab23. 下列等式正确的是( )A、a4+a5=a9 B、a3•a3•a3=3a3 C、2a4•3a5=6a9 D、(﹣a3)4=a74. 下列各组线段不能组成三角形的是( )A、4cm、4cm、5cm B、4cm、6cm、11cm C、4cm、5cm、6cm D、5cm、12cm、13cm5. 若a=0.32 , b=﹣3﹣2 , c=(﹣3)0 , 那么a、b、c三数的大小为( )A、a>c>b B、a>b>c C、c>b>a D、c>a>b6. 一个多边形的内角和是900°,则这个多边形的边数为 ( )A、6 B、7 C、8 D、97. 下列图形中,由 ,能得到 的是( )A、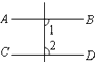 B、
B、 C、
C、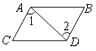 D、
D、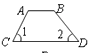 8. 下面的多项式中,能因式分解的是( )A、m2+n2 B、m2+4m+1 C、m2-n D、m2-2m+19. 有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为( )
8. 下面的多项式中,能因式分解的是( )A、m2+n2 B、m2+4m+1 C、m2-n D、m2-2m+19. 有5张边长为2的正方形纸片,4张边长分别为2、3的矩形纸片,6张边长为3的正方形纸片,从其中取出若干张纸片,且每种纸片至少取一张,把取出的这些纸片拼成一个正方形(原纸张进行无空隙、无重叠拼接),则拼成正方形的边长最大为( ) A、6 B、7 C、8 D、910. 下列叙述中,正确的有( )
A、6 B、7 C、8 D、910. 下列叙述中,正确的有( )①如果 ,那么 ;②满足条件 的n不存在;
③任意一个三角形的三条高所在的直线相交于一点,且这点一定在三角形的内部;
④ΔABC中,若∠A+∠B=2∠C,∠A-∠C=40°,则这个△ABC为钝角三角形.
A、0个 B、1个 C、2个 D、3个二、填空题
-
11. 计算:2a﹒a2=.12. 某种物体的长度为0.000000023m,用科学记数法表示为m.13. 已知 , ,则 =.14. 若x2+(a-2)x+9是一个完全平方式,则a=.15. 若化简(x+1)(2x+m)的结果中x的一次项系数是-5,则数m的值为.16. 如图,把 沿线段 折叠,使点 落在点 处, ,若∠A+∠B=110°,则 =.
 17. 如图,两个正方形边长分别为a、b,如果a+b=20,ab=18,则阴影部分的面积为.
17. 如图,两个正方形边长分别为a、b,如果a+b=20,ab=18,则阴影部分的面积为. 18. 如图,长方形ABCD中,AB=12cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x=时,△APE的面积等于16.
18. 如图,长方形ABCD中,AB=12cm,BC=8cm,点E是CD的中点,动点P从A点出发,以每秒2cm的速度沿A→B→C→E运动,最终到达点E.若点P运动的时间为x秒,那么当x=时,△APE的面积等于16.
三、解答题
-
19. 计算:(1)、∣—6∣+( —3.14)0—( )-2+(—2)3(2)、(-a)3•a2+(2a4)2÷a3(3)、(4)、(a-2b)(a+b)-3a(a+b)20. 因式分解(1)、(2)、4x2—16xy+16y2(3)、(y﹣1)2+6(1﹣y)+921.(1)、先化简,再求值:(x-3)2+2(x-2)(x+7)-(x+2)(x-2);其中x2+2x-3=0(2)、已知 ,求: 的值.22. 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
 (1)、请画出平移后的△DEF.(2)、若连接AD、CF,则这两条线段之间的关系是.(3)、画出△ABC的BC边上的高AM。(4)、满足三角形ACP的面积等于三角形ACB的面积的格点P有 个(不和B重合)23. 如图,直角△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F.
(1)、请画出平移后的△DEF.(2)、若连接AD、CF,则这两条线段之间的关系是.(3)、画出△ABC的BC边上的高AM。(4)、满足三角形ACP的面积等于三角形ACB的面积的格点P有 个(不和B重合)23. 如图,直角△ABC中,∠ACB=90°,CD⊥AB于D,CE平分∠ACB交AB于E,EF⊥AB交CB于F. (1)、求证:CD∥EF;(2)、若∠FEC=25°,求∠A的度数.24. 观察下列各式:
(1)、求证:CD∥EF;(2)、若∠FEC=25°,求∠A的度数.24. 观察下列各式:1×5+4=32…………①
3×7+4=52…………②
5×9+4=72…………③
……
探索以上式子的规律:
(1)、试写出第6个等式;(2)、试写出第n个等式(用含n的式子表示),并用你所学的知识说明第n个等式成立.25. 某同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.在图①中,∠B=90°,∠A=30°;图②中,∠D=90°,∠F=45°.图③是该同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合). (1)、在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐;连接FC,∠FCE的度数逐渐.(填“不变”、“变大”或“变小”)(2)、△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;(3)、能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.26. 如图①, 平分 , ⊥ ,∠B=450 , ∠C=730.
(1)、在△DEF沿AC方向移动的过程中,该同学发现:F、C两点间的距离逐渐;连接FC,∠FCE的度数逐渐.(填“不变”、“变大”或“变小”)(2)、△DEF在移动的过程中,∠FCE与∠CFE度数之和是否为定值,请加以说明;(3)、能否将△DEF移动至某位置,使F、C的连线与AB平行?若能,求出∠CFE的度数;若不能,请说明理由.26. 如图①, 平分 , ⊥ ,∠B=450 , ∠C=730. (1)、求 的度数;(2)、如图②,若把“ ⊥ ”变成“点F在DA的延长线上, ”,其它条件不变,求 的度数;(3)、如图③,若把“ ⊥ ”变成“ 平分 ”,其它条件不变, 的大小是否变化,并请说明理由.
(1)、求 的度数;(2)、如图②,若把“ ⊥ ”变成“点F在DA的延长线上, ”,其它条件不变,求 的度数;(3)、如图③,若把“ ⊥ ”变成“ 平分 ”,其它条件不变, 的大小是否变化,并请说明理由.