江苏省海安县八校联考2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2019-06-25 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的图案分别是大众、奥迪、奔驰、三菱汽车的车标，其中，可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 下列实数 $3 π ，－ \frac{7}{8} ， 0 ， \sqrt{2} ，－ 3.15 ， \sqrt{9} ， \frac{\sqrt{3}}{3} ，－ 1.414114111 \cdot \cdot \cdot$ ，中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 下列说法，其中错误的有（）
①相等的两个角是对顶角；②若∠1+∠2＝180°，则∠1与∠2互为补角；③同位角相等；④垂线段最短：⑤同一平面内，两条直线的位置关系有：相交，平行和垂直⑥过直线外一点，有且只有一条直线与这条直线平行

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 点P（m+3，m+1）在x轴上，则点P的坐标为（）

A、(2,0) B、(0，-2) C、(4,0) D、(0，-4)

查看试题解析
5. 若关于 $x, y$ 的二元一次方程组 ${\begin{cases} x + y = 5 k \\ x - y = 9 k \end{cases}$ 的解也是二元一次方程 $2 x + 3 y = 6$ 的解，则 $k$ 的值为（）

A、 $\frac{3}{4}$ B、 $- \frac{3}{4}$ C、 $\frac{4}{3}$ D、 $- \frac{4}{3}$

查看试题解析
6. 将一副三角板如图放置，使点A在DE上，BC∥DE，则∠ACE的度数为（）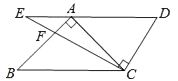

A、10° B、15° C、20° D、25°

查看试题解析
7. 已知平面内不同的两点A（a+2，4）和B（3，2a+2）到x轴的距离相等，则a的值为（）

A、﹣3 B、﹣5 C、1或﹣3 D、1或﹣5

查看试题解析
8. 解方程组 ${\begin{matrix} a x + b y = 2 \\ c x － 7 y = 8 \end{matrix}$ 时，某同学把c看错后得到 ${\begin{matrix} x = － 2 \\ y = 2 \end{matrix}$ ，而正确的解是 ${\begin{matrix} x = 3 \\ y = － 2 \end{matrix}$ ，那么a，b，c的值是（）

A、a＝4，b＝5，c＝2 B、a，b，c的值不能确定 C、a＝4，b＝5，c＝－2 D、a，b不能确定，c＝－2

查看试题解析
9. 规定用符号[m]表示一个实数m的整数部分，例如：[ $\frac{2}{3}$ ]=0，[3.14]=3.按此规定[－ $\sqrt{10}$ ＋1]的值为（）

A、－4 B、－3 C、－2 D、1

查看试题解析
10. 如图，在平面直角坐标系xOy中，点P（1，0）．点P第1次向上跳动1个单位至点P₁（1，1），紧接着第2次向左跳动2个单位至点P₂（－1，1），第3次向上跳动1个单位至点P₃ ，第4次向右跳动3个单位至点P₄ ，第5次又向上跳动1个单位至点P₅ ，第6次向左跳动4个单位至点P₆ ， ……．照此规律，点P第100次跳动至点P₁₀₀的坐标是（）

A、（－26，50） B、（－25，50） C、（26，50） D、（25，50）

查看试题解析

二、填空题

11. $27$ 的立方根是．

查看试题解析
12. 若3x²ⁿy^m与x⁴^﹣ⁿyⁿ^﹣¹是同类项，则m+n= ．

查看试题解析
13. 在平面直角坐标系中，将P向右平移2个单位，再向下平移2个单位得点P′(－3，2)，则点P的坐标为.

查看试题解析
14. 由方程组 ${\begin{matrix} x + m = 6 \\ y - 3 = m \end{matrix}$ ，可得到x与y的关系式是．

查看试题解析
15. 已知直线a平行于x轴，点M(－2，－3)是直线a上的一个点.若点N也是直线a上的一个点，MN=5，则点N的坐标为.

查看试题解析
16. 如图，直线a平移后得到直线b，∠1＝60°，∠B＝130°，则∠2＝°.

查看试题解析
17. 如果∠α与∠β的两边分别平行，∠α比∠β的3倍少36°，则∠α的度数是.

查看试题解析
18. 无论m为何值，点A(m，5－2m)不可能在第象限.

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{0.64} － 2 \sqrt{2 \frac{1}{4}} + \sqrt[3]{64}$

(2)、 $\sqrt[3]{－ 27} － | \sqrt{2} － 2 | + 2 \sqrt{2} －（－ \sqrt{16} ）$

查看试题解析
20. 解下列方程组

(1)、 ${\begin{matrix} 3 x = y + 7 \\ 5 x + 2 y = 8 \end{matrix}$

(2)、 ${\begin{matrix} \frac{m}{2} + \frac{n}{3} = 13 ， \\ \frac{m}{3} － \frac{n}{4} = 3. \end{matrix}$

查看试题解析
21. 已知（2a﹣1）的平方根是±3，（3a+b﹣1）的平方根是±4，求a+2b的平方根.

查看试题解析
22. 已知：如图， $A D / / B E$ ， $∠ 1 = ∠ 2$ ，求证： $∠ A = ∠ E$ .

查看试题解析
23. △ABC在平面直角坐标系中，且A $(- 2 ， 1)$ 、B $(- 3 ， - 2)$ 、C $(1 ， - 4)$ .将其平移后得到 $Δ A_{1} B_{1} C_{1}$ ，若A，B的对应点是 $A_{1}$ ， $B_{1}$ ，C的对应点 $C_{1}$ 的坐标是 $(3 ， - 1)$ .

(1)、在平面直角坐标系中画出△ABC；

(2)、写出点 $A_{1}$ 的坐标是， $B_{1}$ 坐标是；

(3)、此次平移也可看作 $Δ A_{1} B_{1} C_{1}$ 向平移了个单位长度，再向平移了个单位长度得到△ABC.

查看试题解析
24. 先阅读，然后解方程组.
解方程组 ${\begin{matrix} x - y - 1 = 0 ， ① \\ 4 (x - y) - y = 5 ② \end{matrix}$ 时，可由①得 $x - y = 1.$ ③，然后再将③代入②

得 $4 \times 1 - y = 5$ ，求得 $y = - 1$ ，从而进一步求得 ${\begin{matrix} x = 0 ， \\ y = - 1. \end{matrix}$ 这种方法被称为“整体代入法”，

请用这样的方法解下列方程组：

${\begin{matrix} 2 x - 3 y - 2 = 0 ， \\ \frac{2 x - 3 y + 5}{7} + 2 y = 9. \end{matrix}$

查看试题解析
25. 某校为学生开展拓展性课程，拟在一块长比宽多6m的长方形场地内建造由两个大棚组成的植物养殖区，如图（1），要求两个大棚之间有间隔4m的路，设计方案如图（2），已知每个大棚的周长为44m.

(1)、求每个大棚的长和宽各是多少？

(2)、现有两种大棚造价的方案，方案一是每平方米60元，超过100平方米优惠500元，方案二是每平方米70元，超过100平方米优惠总价的20%，试问选择哪种方案更优惠？

查看试题解析
26. 如图①，在平面直角坐标系中，A（a，0），C（b，2），且满足（a+2）²+ $\sqrt{b - 2}$ =0，过C作CB⊥x轴于B.

(1)、求三角形ABC的面积；

(2)、若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图②所示，求∠AED的度数；

(3)、在y轴上是否存在点P，使得三角形ABC和三角形ABP的面积相等？若存在，求出P点坐标；若不存在，请说明理由.

查看试题解析