重庆市江北新区联盟2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-06-25 类型:期中考试
一、单选题
-
1. 函数 中自变量x的取值范围是 ( )A、x ≤1 B、x ≤-1 C、x ≥ 1 D、x ≥-12. 下列二次根式中,不能与 合并的是( )A、 B、 C、 D、3. 下列四个点中,在函数y=3x+1的图像上的是( )A、(-1,2) B、(0,-1) C、(1,4) D、(2,-7)4. 下列各式计算错误的是( )A、 B、 C、 D、5. 如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
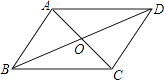 A、AB∥CD,AD∥BC B、OA=OC,OB=OD C、AD=BC,AB∥CD D、AB=CD,AD=BC6. 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
A、AB∥CD,AD∥BC B、OA=OC,OB=OD C、AD=BC,AB∥CD D、AB=CD,AD=BC6. 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )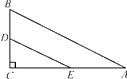 A、1 B、2 C、 D、1+7. 下列说法错误的是( )A、一组对边平行且相等的四边形是平行四边形. B、四条边都相等的四边形是菱形. C、对角线互相垂直的平行四边形是正方形. D、四个角都相等的四边形是矩形8. 下列条件中,不能判断△ABC为直角三角形的是( )A、a=1.5 b=2 c=2.5 B、a:b:c=5:12:13 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:59. 下列三个命题:①对顶角相等;②全等三角形的对应边相等;③如果两个实数是正数,它们的积是正数.它们的逆命题成立的个数是( )A、0个 B、1个 C、2个 D、3个10. 一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )
A、1 B、2 C、 D、1+7. 下列说法错误的是( )A、一组对边平行且相等的四边形是平行四边形. B、四条边都相等的四边形是菱形. C、对角线互相垂直的平行四边形是正方形. D、四个角都相等的四边形是矩形8. 下列条件中,不能判断△ABC为直角三角形的是( )A、a=1.5 b=2 c=2.5 B、a:b:c=5:12:13 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:59. 下列三个命题:①对顶角相等;②全等三角形的对应边相等;③如果两个实数是正数,它们的积是正数.它们的逆命题成立的个数是( )A、0个 B、1个 C、2个 D、3个10. 一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )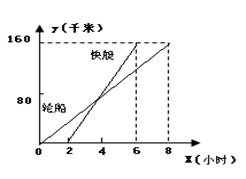 A、轮船的速度为20千米/小时 B、快艇比轮船早到2小时 C、轮船比快艇先出发2小时 D、快艇的速度为 千米/小时11. 如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出( )
A、轮船的速度为20千米/小时 B、快艇比轮船早到2小时 C、轮船比快艇先出发2小时 D、快艇的速度为 千米/小时11. 如图,在4×4方格中作以AB为一边的Rt△ABC,要求点C也在格点上,这样的Rt△ABC能作出( )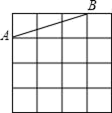 A、2个 B、3个 C、4个 D、6个12. 如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P、P′分别是EF、E′F′的中点,当点A′与点B重合时,四边形PP′F′F的面积为( )
A、2个 B、3个 C、4个 D、6个12. 如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△AEF沿点A到点B的方向平移,得到△A′E′F′.设P、P′分别是EF、E′F′的中点,当点A′与点B重合时,四边形PP′F′F的面积为( )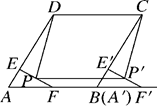 A、8 B、4 C、12 D、8 -8
A、8 B、4 C、12 D、8 -8二、填空题
-
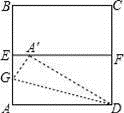
13. 计算:(3+ )(3- )= .14. 使代数式 有意义的x的取值范围是.15. 若一直角三角形的两边为3和4,则它第三边的长为.16. 已知 ,则x-y的值为.17. 如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=cm.
 18. 如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3 , 则S1+S2+S3=.
18. 如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3 , 则S1+S2+S3=.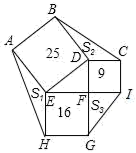
三、解答题
-
19. 计算:(1)、( + + 5)÷ - × - ;(2)、(-3)﹣2 + -|1-2 |-( -3)020. 如图,已知平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过B点作AC的平行线,交CE的延长线于点F,连接BF。
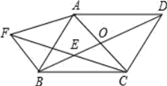 (1)、求证:FB=AO;(2)、平行四边形ABCD满足什么条件时,四边形AFBO是矩形?说明理由.21. 先化简,再求值(其中 x= -2 )22. 一农民带了若干千克自产的萝卜进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出萝卜千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)、求证:FB=AO;(2)、平行四边形ABCD满足什么条件时,四边形AFBO是矩形?说明理由.21. 先化简,再求值(其中 x= -2 )22. 一农民带了若干千克自产的萝卜进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出萝卜千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题: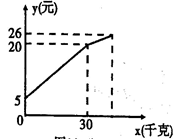 (1)、降价前他每千克萝卜出售的价格是多少?(2)、降价后他按每千克0.4元将剩余萝卜售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克萝卜?23. 在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
(1)、降价前他每千克萝卜出售的价格是多少?(2)、降价后他按每千克0.4元将剩余萝卜售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克萝卜?23. 在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒. (1)、请你帮助他们算一算,这辆小车是否超速?(参考数据: ≈1.41, ≈1.73,计算结果保留两位小数).(2)、请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)24. 已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.
(1)、请你帮助他们算一算,这辆小车是否超速?(参考数据: ≈1.41, ≈1.73,计算结果保留两位小数).(2)、请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)24. 已知平行四边形ABCD中,G为BC中点,点E在AD边上,且∠1=∠2.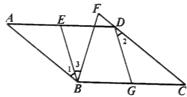 (1)、求证:E是AD中点;(2)、若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.25. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形。例如:某三角形三边长分别是5,6和8,因为 ,所以这个三角形是常态三角形。
(1)、求证:E是AD中点;(2)、若F为CD延长线上一点,连接BF,且满足∠3=∠2,求证:CD=BF+DF.25. 我们新定义一种三角形:两边平方和等于第三边平方的4倍的三角形叫做常态三角形。例如:某三角形三边长分别是5,6和8,因为 ,所以这个三角形是常态三角形。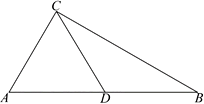 (1)、若△ABC三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是”);(2)、若Rt△ABC是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,若△BCD是常态三角形,求△ABC的面积。26. 在平面直角坐标系中,点A(0,a)、B(b,0).
(1)、若△ABC三边长分别是2, 和4,则此三角形常态三角形(填“是”或“不是”);(2)、若Rt△ABC是常态三角形,则此三角形的三边长之比为(请按从小到大排列);(3)、如图,Rt△ABC中,∠ACB=90°,BC=6,点D为AB的中点,连接CD,若△BCD是常态三角形,求△ABC的面积。26. 在平面直角坐标系中,点A(0,a)、B(b,0).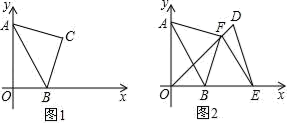 (1)、若a、b满足a2+b2﹣8a﹣4b+20=0.如图,在第一象限内以AB为斜边作等腰Rt△ABC,请求四边形AOBC的面积S;(2)、如图,若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF,判断AF与BF的关系,并说明理由.
(1)、若a、b满足a2+b2﹣8a﹣4b+20=0.如图,在第一象限内以AB为斜边作等腰Rt△ABC,请求四边形AOBC的面积S;(2)、如图,若将线段AB沿x轴向正方向移动a个单位得到线段DE(D对应A,E对应B)连接DO,作EF⊥DO于F,连接AF、BF,判断AF与BF的关系,并说明理由.