江苏省泰兴市黄桥教育联盟2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2019-06-25 类型：期中考试

进入出卷网下载

一、单选题

1. 为了了解某县七年级9800名学生的视力情况，从中抽查了100名学生的视力，就这个问题来说，下列说法正确的是（）

A、9800名学生是总体 B、每个学生是个体 C、100名学生是所抽取的一个样本 D、样本容量是100

查看试题解析
2. 下列图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列各式： $\frac{1}{5} x, \frac{4 x}{π}, \frac{x^{2} - y^{2}}{2}, \frac{1}{x}$ 其中分式共有（）个.

A、1 B、2 C、3 D、4

查看试题解析
4. 如果 $\sqrt{12}$ 与最简二次根式 $\sqrt{7 - 2 a}$ 是同类二次根式，那么a的值是（）

A、﹣2 B、﹣1 C、1 D、2

查看试题解析
5. 如果把分式 $\frac{x^{2}}{3 x + 2 y}$ 中的x和y都扩大为原来的5倍，那么分式的值（）

A、扩大为原来的5倍 B、扩大为原来的10倍 C、不变 D、缩小为原来的 $\frac{1}{5}$

查看试题解析
6. 如图，P为边长为2的正方形ABCD的对角线BD上任一点，过点P作PE⊥BC于点E，PF⊥CD于点F，连接EF.给出以下4个结论：①AP=EF；②AP⊥EF；③EF最短长度为 $\sqrt{2}$ ；④若∠BAP=30°时，则EF的长度为2.其中结论正确的有（）

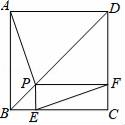A、①②③ B、①②④ C、②③④ D、①③④

查看试题解析

二、填空题

7. 某口袋中有红色、黄色、黑色的小球共50个，这些小球除颜色外都相同，通过多次试验后发现摸到红色球的频率稳定在20%，则袋中红色球是个．

查看试题解析
8. 若分式 $\frac{x^{2} - 1}{x - 1}$ 的值为零，则x= ．

查看试题解析
9. 如图，在平行四边形ABCD中，DE平分∠ADC，AD=6，BE=2，则平行四边形ABCD的周长是.

查看试题解析
10. 计算： $1 - \frac{a - b}{a + b}$ = .

查看试题解析
11. 若分式方程 $\frac{1}{x - 3} + 1 = \frac{a - x}{x - 3}$ 有增根，则 $a$ 的值是

查看试题解析
12. 如果△ABC的三条中位线分别为3cm，4cm，5cm，那么△ABC的周长为cm．

查看试题解析
13. 如图，在Rt△ABC中，∠C=90°，BC=5，AC=12，M为斜边AB上一动点，过M作MD⊥AC，过M作ME⊥CB于点E，则线段DE的最小值为.

查看试题解析
14. △ABC中a，b，c为三角形的三边，则 $\sqrt{{(a - b + c)}^{2}} - 2 | c - a - b | =$ .

查看试题解析
15. 关于x的方程 $\frac{2 x + a}{x - 2} = 1$ 的解是大于1的数，则a的取值范围是

查看试题解析
16. 如图，在菱形ABCD中，对角线AC、BD相交于点O，点E是线段BO上的一个动点（可以与O、B重合），点F为射线DC上一点，若∠ABC=60∘，∠AEF=120∘，AB=5，则EF的取值范围是.

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{12} \times \frac{\sqrt{3}}{3} - {(\sqrt{3} - 1)}^{0} + | - 3 |$

(2)、 $(3 \sqrt{18} + \frac{1}{5} \sqrt{50} - 4 \sqrt{\frac{1}{2}}) \div \sqrt{32}$

查看试题解析
18. 化简：

(1)、 $1 - \frac{x - y}{x + 2 y} \div \frac{x^{2} - y^{2}}{x^{2} + 4 x y + 4 y^{2}}$

(2)、 $\frac{x^{2}}{x + 1}$ ﹣x+1

查看试题解析
19. 解方程：

(1)、 $\frac{2}{x - 2} - \frac{1}{x} = 0$ ；

(2)、 $\frac{x}{x - 1} - 1 = \frac{2}{x^{2} - 1}$

查看试题解析
20. 先化简再求值：化简 $\frac{m - 2}{m^{2} - 1} \div (\frac{m^{2} - m}{m^{2} - 2 m + 1} - \frac{2}{m - 1})$ ，并0，-1，1，2四个数中，取一个合适的数作为m的值代入求值.

查看试题解析
21. 吸烟有害健康.你知道吗，被动吸烟也大大危害着人类的健康.为此，联合国规定每年的5月31日为世界无烟日.为配合今年的“世界无烟日”宣传活动，小明和同学们在学校所在地区展开了以“我支持的戒烟方式”为主题的问卷调查活动，征求市民的意见，并将调查结果分析整理后，制成下列统计图：

(1)、求小明和同学们一共随机调查了多少人？

(2)、根据以上信息，请你把统计图补充完整；

(3)、如果该地区有2万人，那么请你根据以上调查结果，估计该地区大约有多少人支持“强制戒烟”这种戒烟方式？

查看试题解析
22. 如图，已知△ABC的三个顶点坐标为A（﹣2，3），B（﹣6，0），C（﹣1，0）.

(1)、将△ABC绕坐标原点O旋转180°，画出图形，并写出点A的对应点A′的坐标；

(2)、将△ABC绕坐标原点O逆时针旋转90°，直接写出点A的对应点A″的坐标；

(3)、请直接写出：以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标.

查看试题解析
23. 某篮球运动员去年共参加40场比赛，其中3分球的命中率为0.25，平均每场有12次3分球未投中．

(1)、该运动员去年的比赛中共投中多少个3分球？

(2)、在其中的一场比赛中，该运动员3分球共出手20次，小亮说，该运动员这场比赛中一定投中了5个3分球，你认为小亮的说法正确吗？请说明理由．

查看试题解析
24. 如图，在四边形ABCD中，AB=BC ，对角线BD平分∠ABC ， P是BD上一点，过点P作PM⊥AD ， PN⊥CD ，垂足分别为M、N.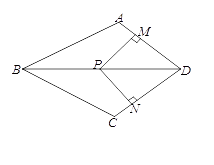

(1)、求证：∠ADB=∠CDB；

(2)、若∠ADC=90°，求证：四边形MPND是正方形.

查看试题解析
25. 如图，等边 ABC 的边长是 2 ， D、E 分别为 AB 、 AC 的中点，连接CD ，过 E 点作 EF // DC 交 BC 的延长线于点 F

(1)、求证：四边形 CDEF 是平行四边形；

(2)、求四边形 CDEF 的周长

查看试题解析
26. 如图，在平面直角坐标系中，直线y= $\frac{4}{3}$ x+4分别交x轴，y轴于A，B两点，点C为OB的中点，点D在第二象限，且四边形AOCD为矩形.

(1)、直接写出点A，B的坐标，并求直线AB与CD交点E的坐标；

(2)、动点P从点C出发，沿线段CD以每秒1个单位长度的速度向终点D运动；同时，动点N从点A出发，沿线段AO以每秒1个单位长度的速度向终点O运动，过点P作PH⊥OA，垂足为H，连接NP.设点P的运动时间为t秒.
①若△NPH的面积为1，求t的值；

②点Q是点B关于点A的对称点，问BP+PH+HQ是否有最小值，如果有，求出相应的点P的坐标；如果没有，请说明理由.

查看试题解析