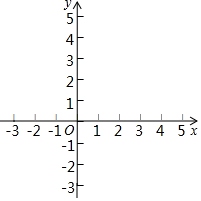广西玉林市陆川县2018-2019学年八年级下学期期中考试数学试题
试卷更新日期:2019-06-25 类型:期中考试
一、单选题
-
1. 下列各式中,一定是二次根式的是A、 B、 C、 D、2. 若二次根式 有意义,则x的取值范围是( )A、x> B、x≥ C、x≤ D、x≤53. 下列式子为最简二次根式的是( )A、 B、 C、 D、4. 下列各式计算正确的是( )A、 B、 C、 D、5. 下列二次根式能 合并的是( )A、 B、 C、 D、6. 将下列长度的三根木棒首尾顾次连接,能构成直角三角形的是( )A、6,8,12 B、 C、5,12,13 D、7. 下列说法中正确的是( )A、两条对角线互相垂直的四边形是菱形 B、两条对角线互相平分的四边形是平行四边形 C、两条对角线相等的四边形是矩形 D、两条对角线互相垂直且相等的四边形是正方形8. 我国是最早了解勾股定理的国家之一 下面四幅图中,不能证明勾股定理的是A、
 B、
B、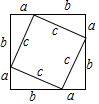 C、
C、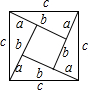 D、
D、 9. 顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是( )A、平行四边形 B、菱形 C、矩形 D、正方形10. 若式子 的值为2,那么a的取值范围是( )A、a≤4 B、a≥2 C、a=2或a=4 D、2≤a≤411. 如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE⊥AC于E,PF⊥BC于点F,连结EF,则线段EF的最小值为( )
9. 顺次连接一个四边形的各边中点,得到了一个正方形,则这个四边形最可能是( )A、平行四边形 B、菱形 C、矩形 D、正方形10. 若式子 的值为2,那么a的取值范围是( )A、a≤4 B、a≥2 C、a=2或a=4 D、2≤a≤411. 如图,在△ABC中,∠C=90°,AC=8,BC=6,点P为斜边AB上一动点,过点P作PE⊥AC于E,PF⊥BC于点F,连结EF,则线段EF的最小值为( ) A、24 B、 C、 D、5
A、24 B、 C、 D、5二、填空题
-
12. 如图,△ABC中,AB=AC,AB=5,BC=8,AD是∠BAC的平分线,则AD的长为.
 13. 计算:14. 已知一个直角三角形的两边长分别为3和4,则斜边长为 .15. 若 =3﹣x,则x的取值范围是 .16. 已知矩形的面积为S,相邻两边长分别为a,b,已知S=2 ,a= ,则b=.17. 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(5,0)、(0,4),点P是线段BC上的动点,当△PBA是等腰三角形时,则P点的坐标是.
13. 计算:14. 已知一个直角三角形的两边长分别为3和4,则斜边长为 .15. 若 =3﹣x,则x的取值范围是 .16. 已知矩形的面积为S,相邻两边长分别为a,b,已知S=2 ,a= ,则b=.17. 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(5,0)、(0,4),点P是线段BC上的动点,当△PBA是等腰三角形时,则P点的坐标是. 18. 如图,在边长为1的正方形ABCD中,等边△AEF的顶点E、F分别在边BC和CD上则下列结论:①CE=CF:②∠AEB=75°;③S△EFC=1;④ ,其中正确的有(用序号填写)
18. 如图,在边长为1的正方形ABCD中,等边△AEF的顶点E、F分别在边BC和CD上则下列结论:①CE=CF:②∠AEB=75°;③S△EFC=1;④ ,其中正确的有(用序号填写)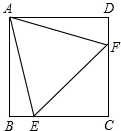
三、解答题
-
19. 计算(1)、(2)、20. 已知:如图,Rt△ABC中,∠C=90°,AC= ,BC= ,求
 (1)、Rt△ABC的面积.(2)、斜边AB的长.(3)、求AB边上的高.21. 如图,在▱ABCD中,E、F分别是BC、AD边上的点,且∠1=∠2.求证:四边形AECF是平行四边形.
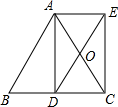
(1)、Rt△ABC的面积.(2)、斜边AB的长.(3)、求AB边上的高.21. 如图,在▱ABCD中,E、F分别是BC、AD边上的点,且∠1=∠2.求证:四边形AECF是平行四边形. 22. 如图,AD是等腰△ABC底边BC上的中线,点O是AC中点,延长DO到E,使OE=OD,连接AE,CE,求证:四边形ADCE的是矩形.
22. 如图,AD是等腰△ABC底边BC上的中线,点O是AC中点,延长DO到E,使OE=OD,连接AE,CE,求证:四边形ADCE的是矩形.