甘肃省兰州市第四片区2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-06-25 类型:期中考试
一、单选题
-
1. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若等腰三角形的顶角为 ,则它的底角度数为( )A、40 B、50 C、60 D、653. 把不等式组 的解集表示在数轴上,下列不符合题意的是( )A、
2. 若等腰三角形的顶角为 ,则它的底角度数为( )A、40 B、50 C、60 D、653. 把不等式组 的解集表示在数轴上,下列不符合题意的是( )A、 B、
B、 C、
C、 D、
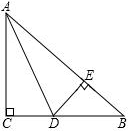
D、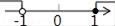 4. 在平面直角坐标系中,点A(2,5)与点B关于原点对称,则点B的坐标是( )A、(﹣5,﹣2) B、(2,﹣5) C、(﹣2,5) D、(﹣2,﹣5)5. 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
4. 在平面直角坐标系中,点A(2,5)与点B关于原点对称,则点B的坐标是( )A、(﹣5,﹣2) B、(2,﹣5) C、(﹣2,5) D、(﹣2,﹣5)5. 如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )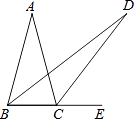 A、15° B、17.5° C、20° D、22.5°6. 下列说法正确的是( )A、平移不改变图形的形状和大小,而旋转则改变图形的形状和大小 B、在成中心对称的两个图形中,连结对称点的线段都被对称中心平分 C、在平面直角坐标系中,一点向右平移2个单位,纵坐标加2 D、在平移和旋转图形中,对应角相等,对应线段相等且平行7. 如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
A、15° B、17.5° C、20° D、22.5°6. 下列说法正确的是( )A、平移不改变图形的形状和大小,而旋转则改变图形的形状和大小 B、在成中心对称的两个图形中,连结对称点的线段都被对称中心平分 C、在平面直角坐标系中,一点向右平移2个单位,纵坐标加2 D、在平移和旋转图形中,对应角相等,对应线段相等且平行7. 如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )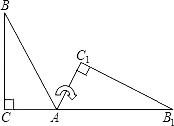 A、55° B、70° C、125° D、145°8. 已知不等式组 有解,则 的取值范围为( )A、a>-2 B、a≥-2 C、a<2 D、a≥29. 如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么∠ABC的大小是( )
A、55° B、70° C、125° D、145°8. 已知不等式组 有解,则 的取值范围为( )A、a>-2 B、a≥-2 C、a<2 D、a≥29. 如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么∠ABC的大小是( ) A、40° B、45° C、50° D、60°10. 如图,在△ABC中,∠B=32°,∠BAC的平分线AD交BC于点D,若DE垂直平分AB,则∠C的度数为( )
A、40° B、45° C、50° D、60°10. 如图,在△ABC中,∠B=32°,∠BAC的平分线AD交BC于点D,若DE垂直平分AB,则∠C的度数为( )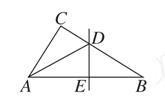 A、90° B、84° C、64° D、58°11. 如图, 是等边 内一点, , , ,将线段 以点 为旋转中心逆时针旋转 得到线段 ,下列结论:
A、90° B、84° C、64° D、58°11. 如图, 是等边 内一点, , , ,将线段 以点 为旋转中心逆时针旋转 得到线段 ,下列结论:① 可以由 绕点 逆时针旋转 得到;②点 与 的距离为 ;③四边形 的面积为 ④ ;⑤ .
其中正确的结论是( )
 A、②③④⑤ B、①③④⑤ C、①②③⑤ D、①②④⑤
A、②③④⑤ B、①③④⑤ C、①②③⑤ D、①②④⑤二、填空题
-
12. 一个等腰三角形的两边长分别为2和5,则它的周长为。13. 如图,在 中, , , 平分 ,交 于点 ,若 ,则 .
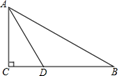 14. 不等式 的解集为.15. 一次函数 y=kx+b 的图像如图所示,则当kx+b>0 时,x 的取值范围为.
14. 不等式 的解集为.15. 一次函数 y=kx+b 的图像如图所示,则当kx+b>0 时,x 的取值范围为.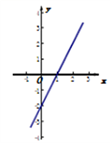 16. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .
16. 如图,矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为 .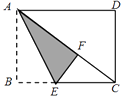
三、解答题
-
17. 解不等式 ,并把解表示在数轴上.18. 解不等式组19. 如图,在 中, , .
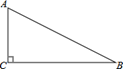 (1)、作边 的中垂线交 边于点 ,交 边于点 (尺规作图,不写作法,保留作图痕迹).(2)、连接 ,若 ,求 的长.20. 如图,在平面直角坐标系中, 的三个顶点分别为 , , .
(1)、作边 的中垂线交 边于点 ,交 边于点 (尺规作图,不写作法,保留作图痕迹).(2)、连接 ,若 ,求 的长.20. 如图,在平面直角坐标系中, 的三个顶点分别为 , , .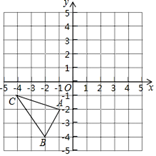
①把 向上平移 个单位后得到 ,请画出 ;
②已知点 与点 关于直线 成轴对称,请画出直线 及 关于直线 对称的 .
③在 轴上存在一点 ,满足点 到点 与点 距离之和最小,请直接写出 点的坐标.
21. 如图,已知 中, , , ,分别以 、 两点为圆心,大于 的长为半径画弧,两弧分别相交于 、 两点,直线 交 于点 ,求 的长.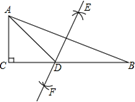 22. 已知 是关于 的不等式 的解,求 的取值范围。23. 如图,在 中, , ,点 在 上,且 ,点 在 的延长线上,且 .求 的度数.
22. 已知 是关于 的不等式 的解,求 的取值范围。23. 如图,在 中, , ,点 在 上,且 ,点 在 的延长线上,且 .求 的度数.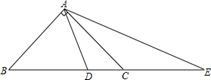 24. 如图,等腰 中, , ,角平分线 ,点 是 中点,求 的长.
24. 如图,等腰 中, , ,角平分线 ,点 是 中点,求 的长. 25. 近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.(1)、求每台A种、B种设备各多少万元?(2)、根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?
25. 近年来,雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注,某学校计划在教室内安装空气净化装置,需购进A、B两种设备,已知:购买1台A种设备和2台B种设备需要3.5万元;购买2台A种设备和1台B种设备需要2.5万元.(1)、求每台A种、B种设备各多少万元?(2)、根据学校实际,需购进A种和B种设备共30台,总费用不超过30万元,请你通过计算,求至少购买A种设备多少台?