甘肃省靖远县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2019-06-25 类型:期中考试
一、单选题
-
1. “x的3倍与2的差不大于7”列出不等式是( )A、3x-2>7 B、3x-2<7 C、3x-2≥7 D、3x-2≤72. 如果一个等腰三角形的两边长为4、9,则它的周长为( )A、17 B、22 C、17或22 D、无法计算3. 在数轴上表示不等式x>-2的解集,正确的是( )A、
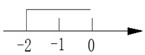 B、
B、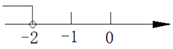 C、
C、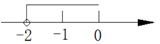 D、
D、 4. 如图,等边三角形ABC的边长为4,则点C的坐标是( )
4. 如图,等边三角形ABC的边长为4,则点C的坐标是( )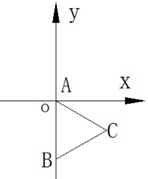 A、(4,-2) B、(4,2) C、(-2, ) D、(2 ,-2)5. 若不等式组 有解集,则m的取值范围是( )A、m<11 B、m>11 C、m≤11 D、m≥116. 时间经过25分钟,钟表的分针旋转了( )A、150° B、120° C、25° D、12.5°7. 如图在△ABC中,BC=8,AB,AC的垂直平分线与BC分别交于E,F两点,则△AEF的周长为( )
A、(4,-2) B、(4,2) C、(-2, ) D、(2 ,-2)5. 若不等式组 有解集,则m的取值范围是( )A、m<11 B、m>11 C、m≤11 D、m≥116. 时间经过25分钟,钟表的分针旋转了( )A、150° B、120° C、25° D、12.5°7. 如图在△ABC中,BC=8,AB,AC的垂直平分线与BC分别交于E,F两点,则△AEF的周长为( )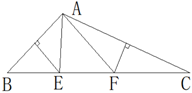 A、2 B、4 C、8 D、不能确定8. 下列图形既是轴对称图形又是中心对称图形的图形是( )A、等腰三角形 B、等边三角形 C、长方形 D、梯形9. 如果kb<0,且不等式kx+b>0解集是x<- ,那么函数y=kx+b的图像只可能是下列的( )A、
A、2 B、4 C、8 D、不能确定8. 下列图形既是轴对称图形又是中心对称图形的图形是( )A、等腰三角形 B、等边三角形 C、长方形 D、梯形9. 如果kb<0,且不等式kx+b>0解集是x<- ,那么函数y=kx+b的图像只可能是下列的( )A、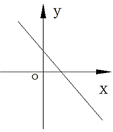 B、
B、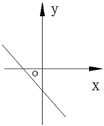 C、
C、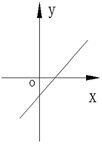 D、
D、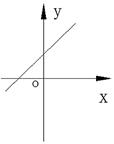
二、填空题
-
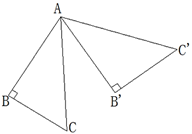
10. 若a、b、c满足(a-5)2+ + =0,则以a,b,c为边的三角形面积是.11. 不等式12-4x≥0的非负整数解是12. “等腰三角形的两底角相等”的逆命题是.13. 如图,在等腰直角三角形ABC中,∠B=90°,将△ABC绕顶点A逆时针方向旋转60°后得到△AB'C',则∠BAC'等于.
 14. 在△ABC中,已知∠A=60°,∠C=90°,AC=5cm,那么AB=.15. 如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB与E,且DE=1.5cm,AC=8cm,BD=2.5cm,则AB=cm.
14. 在△ABC中,已知∠A=60°,∠C=90°,AC=5cm,那么AB=.15. 如图,在△ABC中,∠C=90°,AD是角平分线,DE⊥AB与E,且DE=1.5cm,AC=8cm,BD=2.5cm,则AB=cm.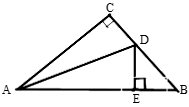 16. 如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC与点E,若三角形BCE的周长等于50,则BC的长为.
16. 如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC与点E,若三角形BCE的周长等于50,则BC的长为. 17. 已知点 M(-2,-5)先向上平移三个单位长度,再向左平移三个单位长度得到点M'的坐标是.18. 已知关于X的不等式组 的解集为-1<x<2,则(m+n)2019的值是.
17. 已知点 M(-2,-5)先向上平移三个单位长度,再向左平移三个单位长度得到点M'的坐标是.18. 已知关于X的不等式组 的解集为-1<x<2,则(m+n)2019的值是.三、解答题
-
19. 如图,AB∥CD,BE平分∠ABC,若∠CDE=150°,则∠C=.
 20. 如图,在网格内有一△ABC,把三角形绕点O顺时针旋转90°,请画出旋转后的△A'B'C'
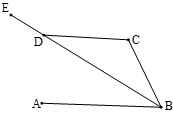
20. 如图,在网格内有一△ABC,把三角形绕点O顺时针旋转90°,请画出旋转后的△A'B'C'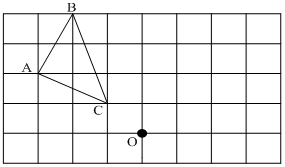 21. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(不写作法,保留作图痕迹).
21. 如图,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(不写作法,保留作图痕迹). 22. 如图.在△ABC中,AD是角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.
22. 如图.在△ABC中,AD是角平分线,且BD=CD,DE⊥AB,DF⊥AC,垂足分别为E、F.求证:EB=FC.
 23. 阅读下面的材料,回答问题:如果(x-2)(6+2x)>0,求x的取值范围.
23. 阅读下面的材料,回答问题:如果(x-2)(6+2x)>0,求x的取值范围.解:根据题意,得 或 ,分别解这两个不等式组,得第一个不等式组的解集为x>2,第二个不等式组的解集为x<-3.故当x>2或x<-3时,(x-2)(6+2x)>0.
(1)、由(x-2)(6+2x)>0,得出不等式组 或 ,体现了思想;(2)、试利用上述方法,求不等式(x-3)(1-x)<0的解集.24. 我校八(2)班共有50名学生,老师安排每人制作一件A型或B型的陶艺品,学校现有甲种制作材料36kg,乙种制作材料29kg,制作A、B两种型号的陶艺品用料情况如下表:需甲种材料
需乙种材料
1件A型陶艺品
0.9kg
0.3kg
1件B型陶艺品
0.4kg
1kg
(1)、设制作B型陶艺品x件,求x的取值范围;(2)、请你根据学校现有的材料,分别写出八(2)班制作A型和B型陶艺品的件数;(3)、若1件A型陶艺品和1件B型陶艺品销售获利分别为10元和15元,利用函数的性质,请分析说明如何制作获得的利润最大,最大利润为多少元?