广东省深圳市2019年中考数学试卷
试卷更新日期:2019-06-24 类型:中考真卷
一、选择题(每小题3分,共12小题,满分36分)
-
1. 的绝对值是( )A、-5 B、 C、5 D、2. 下列图形中是轴对称图形的是( )A、
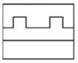 B、
B、 C、
C、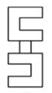 D、
D、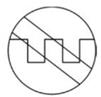 3. 预计到2025年,中国5G用户将超过460000000,将460000000用科学记数法表示为( )A、4.6×109 B、46×107 C、4.6×108 D、0.46×1094. 下列哪个图形是正方体的展开图( )A、
3. 预计到2025年,中国5G用户将超过460000000,将460000000用科学记数法表示为( )A、4.6×109 B、46×107 C、4.6×108 D、0.46×1094. 下列哪个图形是正方体的展开图( )A、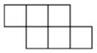 B、
B、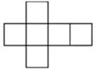 C、
C、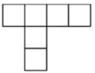 D、
D、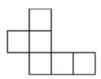 5. 这组数据20,21,22,23,23的中位数和众数分别是( )A、20,23 B、21,23 C、21,22 D、22,236. 下列运算正确的是( )A、a2+a2=a4 B、a3a4=a12 C、(a3)4=a12 D、(ab)2=ab27. 如图,已知l1∥AB,AC为角平分线,下列说法错误的是( )
5. 这组数据20,21,22,23,23的中位数和众数分别是( )A、20,23 B、21,23 C、21,22 D、22,236. 下列运算正确的是( )A、a2+a2=a4 B、a3a4=a12 C、(a3)4=a12 D、(ab)2=ab27. 如图,已知l1∥AB,AC为角平分线,下列说法错误的是( )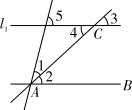 A、∠1=∠4 B、∠1=∠5 C、∠2=∠3 D、∠1=∠38. 如图,已知AB=AC,AB=5,BC=3,以AB两点为圆心,大于 AB的长为半径画圆弧,两弧相交于点M、N,连接MN与AC相交于点D,则△BDC的周长为( )
A、∠1=∠4 B、∠1=∠5 C、∠2=∠3 D、∠1=∠38. 如图,已知AB=AC,AB=5,BC=3,以AB两点为圆心,大于 AB的长为半径画圆弧,两弧相交于点M、N,连接MN与AC相交于点D,则△BDC的周长为( )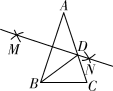 A、8 B、10 C、11 D、139. 已知y=ax2+bx+c(a≠0)的图象如图,则y=ax+b和y= 的图象为( )
A、8 B、10 C、11 D、139. 已知y=ax2+bx+c(a≠0)的图象如图,则y=ax+b和y= 的图象为( )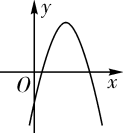 A、
A、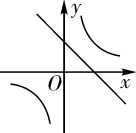 B、
B、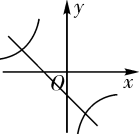 C、
C、 D、
D、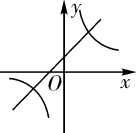 10. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等11. 定义新运算 nxn-1dx=an-bn , 例如 2xdx=k2-h2 , 若-x-2dx=-2.则m=( ).
10. 下面命题正确的是( )A、矩形对角线互相垂直 B、方程x2=14x的解为x=14 C、六边形内角和为540° D、一条斜边和一条直角边分别相等的两个直角三角形全等11. 定义新运算 nxn-1dx=an-bn , 例如 2xdx=k2-h2 , 若-x-2dx=-2.则m=( ).
A、-2 B、 C、2 D、12. 已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论: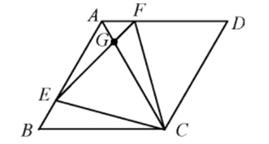
①△BCE≌△ACF②△CEF为正三角形③∠AGE=∠BEC④若AF=1,则EG=3FG正确的有( )个.
A、1 B、2 C、3 D、4二、填空题(每小题3分,共4小题,满分12分)
-
13. 分解因式:ab2-a= .14. 现有8张同样的卡片,分别标有数字:1,1,2,2,2,3,4,5,将这些卡片放在一个不透明的盒子里,搅匀后从中随机地抽出一张,抽到标有数字2的卡片的概率是 .15. 如图,在正方形ABCD中,BE=1,将BC沿CE翻折,使B点对应点刚好落在对角线AC上,将AD沿AF翻折,使D点对应点刚好落在对角线AC上,求EF= .
 16. 如图,在平面直角坐标系中,A(0,-3),∠ABC=90°,y轴平分∠BAC,AD=3CD,若点C在反比例函数y= 上,则k= .
16. 如图,在平面直角坐标系中,A(0,-3),∠ABC=90°,y轴平分∠BAC,AD=3CD,若点C在反比例函数y= 上,则k= .
三、解答题(第17题5分,第18题6分,第19题7分,第20题8分,第21题8分,第22题9分,第23题9分)
-
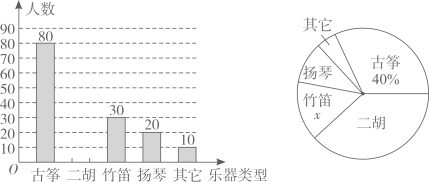
17. 计算: -2cos60°+( )-1+(π-3.14)0 .18. 先化简(1- )÷ ,再将x=-1代入求值。19. 某校为了解学生对中国民族乐器的喜爱情况,随机抽取了本校的部分学生进行调查(每名学生选择并且只能选择一种喜爱的乐器),现将收集的数据绘制成如下两幅不完整的统计图.
 (1)、这次共抽取名学生进行调查,扇形统计图中的x=:(2)、请补全统计图;(3)、在扇形统计图中“扬琴”所对扇形的圆心角是度;(4)、若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有 名.20. 如图所示,某施工队要测量隧道BC长度,已知:AD=600米,AD⊥BC,施工队站在点D处看向B,测得仰角为45°,再由D走到E处测量,DE∥AC,ED=500米,测得仰角为53°,求隧道BC长.(sin53°≈ ,cos53°≈ ,tan53°≈ ).
(1)、这次共抽取名学生进行调查,扇形统计图中的x=:(2)、请补全统计图;(3)、在扇形统计图中“扬琴”所对扇形的圆心角是度;(4)、若该校有3000名学生,请你估计该校喜爱“二胡”的学生约有 名.20. 如图所示,某施工队要测量隧道BC长度,已知:AD=600米,AD⊥BC,施工队站在点D处看向B,测得仰角为45°,再由D走到E处测量,DE∥AC,ED=500米,测得仰角为53°,求隧道BC长.(sin53°≈ ,cos53°≈ ,tan53°≈ ). 21. 有A,B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.(1)、求焚烧1吨垃圾,A和B各发电多少?(2)、A,B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量最大为多少度?22. 如图抛物线经y=ax2+bx+c过点A(-1,0),点C(0,3),且OB=OC.
21. 有A,B两个发电厂,每焚烧一吨垃圾,A发电厂比B发电厂多发40度电,A焚烧20吨垃圾比B焚烧30吨垃圾少1800度电.(1)、求焚烧1吨垃圾,A和B各发电多少?(2)、A,B两个发电厂共焚烧90吨的垃圾,A焚烧的垃圾不多于B焚烧的垃圾两倍,求A厂和B厂总发电量最大为多少度?22. 如图抛物线经y=ax2+bx+c过点A(-1,0),点C(0,3),且OB=OC. (1)、求抛物线的解析式及其对称轴;(2)、点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值;(3)、点P为抛物线上一点,连接CP,直线CP把四边形APBC面积分为3:5两部分,求点P的坐标.23. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.
(1)、求抛物线的解析式及其对称轴;(2)、点D、E在直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值;(3)、点P为抛物线上一点,连接CP,直线CP把四边形APBC面积分为3:5两部分,求点P的坐标.23. 已知在平面直角坐标系中,点A(3,0),B(-3,0),C(-3,8),以线段BC为直径作圆,圆心为E,直线AC交□E于点D,连接OD.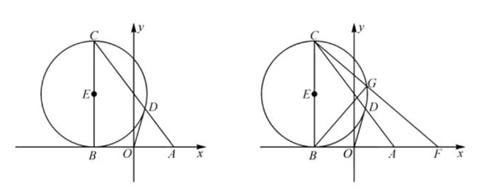 (1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:
(1)、求证:直线OD是□E的切线;(2)、点F为x轴上任意一点,连接CF交□E于点G,连接BG:当tan∠FCA= ,求所有F点的坐标(直接写出);