浙江省台州市2019年中考数学试卷
试卷更新日期:2019-06-21 类型:中考真卷
一、选择题(本题有15小题,每小题4分,共60分)
-
1. 计算2a-3a,结果正确的是( )A、-1 B、1 C、-a D、a2. 如图是某几何体的三视图,则该几何体是( )
 A、长方体 B、正方体 C、圆柱 D、球3. 2019年台州市计划安排重点建设项目344个,总投资595200000000元,用科学记数法可将595200000000表示为( )A、 5.952×1011 B、59.52×1010 C、5.952×1012 D、5952×1094. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,115. 方差是刻画数据波动程度的量,对于一组数据x·x1·…xn , 可用如下算式计算方差s2= [(x1-5)2+(x2-5)2+.…+(xn-5)2],其中“5”是这组数据的( )A、最小值 B、平均数 C、中位数 D、众数6. 一道来自课本的习题:
A、长方体 B、正方体 C、圆柱 D、球3. 2019年台州市计划安排重点建设项目344个,总投资595200000000元,用科学记数法可将595200000000表示为( )A、 5.952×1011 B、59.52×1010 C、5.952×1012 D、5952×1094. 下列长度的三条线段,能组成三角形的是( )A、3,4,8 B、5,6,10 C、5,5,11 D、5,6,115. 方差是刻画数据波动程度的量,对于一组数据x·x1·…xn , 可用如下算式计算方差s2= [(x1-5)2+(x2-5)2+.…+(xn-5)2],其中“5”是这组数据的( )A、最小值 B、平均数 C、中位数 D、众数6. 一道来自课本的习题:从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min,甲地到乙地全程是多少?
小红将这个实际问题转化为二元一次方程组问题,设未知数x,y,已经列出一个方程 ,则另一个方程正确的是( )
A、 B、 C、 D、7. 如图,等边三角形ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O的半径为( ) A、2 B、3 C、4 D、4-8. 如图,有两张矩形纸片ABCD和EFGH、AB=EF=2cm,BC=FG=8cm,把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合,当两张纸片交叉所成的角最小α时,tanα等于( )
A、2 B、3 C、4 D、4-8. 如图,有两张矩形纸片ABCD和EFGH、AB=EF=2cm,BC=FG=8cm,把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合,当两张纸片交叉所成的角最小α时,tanα等于( )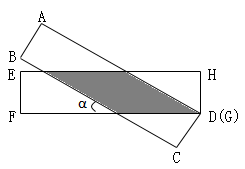 A、 B、 C、 D、9. 已知某函数的图象C与函数y= 的图象关于直线y=2对称下列命题:①图象C与函数y= 的象交于点( ,2);②( ,-2)在图象C上;③图象C上的点的纵坐标都小于4;④A(x1 , y1),B(x2 , y2)是图象C上任意两点,若x1>x2 , 则y1-y2 , 其中真命题是( )A、①② B、①③④ C、②③④ D、①②③④10. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )
A、 B、 C、 D、9. 已知某函数的图象C与函数y= 的图象关于直线y=2对称下列命题:①图象C与函数y= 的象交于点( ,2);②( ,-2)在图象C上;③图象C上的点的纵坐标都小于4;④A(x1 , y1),B(x2 , y2)是图象C上任意两点,若x1>x2 , 则y1-y2 , 其中真命题是( )A、①② B、①③④ C、②③④ D、①②③④10. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )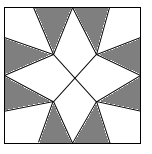 A、 :1 B、3:2 C、 :1 D、 :2
A、 :1 B、3:2 C、 :1 D、 :2二、填空题
-
11. 分解因式:ax2-ay2= .12. 若一个数的平方等于5,则这个数等于。
13. 若一个不透明的布袋中仅有2个红球,1个黑球,这些球除颜色外无其它差别,先随机摸出一个小球,记下颜色后放回搅匀,再随机摸出一个小球,则两次摸出的小球颜色不同的概率是。14. 如图,AC是圆内接四边形ABCD的一条对角线,点D关于AC的对称点E在边BC上连接AE.若∠ABC=64°,则∠BAE的度数为.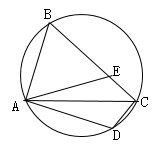 15. 砸金蛋游戏:把210个“金蛋”连续编号为1,2,3,…,210,接着把编号是3的整数倍的“金蛋”全部砸碎,然后将剩下的”金蛋”重新连续编号为1,2,3,…,接着把编号是3的整数倍的“金蛋”全部砸碎…按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止。操作过程中砸碎编号是“66” “金蛋”共个16. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.
15. 砸金蛋游戏:把210个“金蛋”连续编号为1,2,3,…,210,接着把编号是3的整数倍的“金蛋”全部砸碎,然后将剩下的”金蛋”重新连续编号为1,2,3,…,接着把编号是3的整数倍的“金蛋”全部砸碎…按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止。操作过程中砸碎编号是“66” “金蛋”共个16. 如图,直线l1∥l2∥l3 , A,B,C分别为直线l1 , l2 , l3上的动点,连接AB,BC,AC,线段AC交直线l2于点D.设直线l1 , l2之间的距离为m,直线l2 , l3之间的距离为n,若∠ABC=90°,BD=4,且 则m+n的最大值为.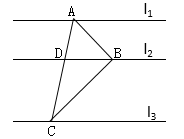
三、解答题
-
17. 计算:18. 先化简,再求值: ,其中x=19. 图1是一辆在平地上滑行的滑板车,图2是其示意图,已知车杆AB长92cm,车杆与脚踏板所成的角∠ABC=70°,前后轮子的半径均为6cm,求把手A离地面的高度(结果保留小数点后一位:参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
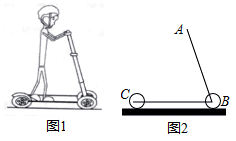 20. 如图1某商场在一楼到二楼之回设有上、下行自动扶梯和步行楼梯、甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系 , 乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图2所示。
20. 如图1某商场在一楼到二楼之回设有上、下行自动扶梯和步行楼梯、甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h(单位:m)与下行时间x(单位:s)之间具有函数关系 , 乙离一楼地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图2所示。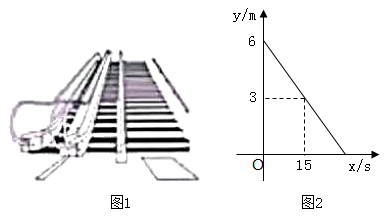 (1)、求y关于x的函数解析式。
(1)、求y关于x的函数解析式。
(2)、请通过计算说明甲、乙两人谁先到达一楼地面。
21. 安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动,在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车安全帽情况进行问卷调查,将收集的数据制成如下统计图表活动前骑电车戴安全帽情况统计表
类别
人数
A
68
B
245
C
510
D
177
合计
1000
活动后骑电车戴安全帽情况统计图
 (1)、宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?(2)、该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不敲”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法22. 我们知道,各个角都相等,各条边都相等的多边形叫做正多边形,对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形
(1)、宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?(2)、该市约有30万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;(3)、小明认为,宣传活动后骑电瓶车“都不敲”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法22. 我们知道,各个角都相等,各条边都相等的多边形叫做正多边形,对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形 (1)、已知凸五边形ABCDE的各条边都相等
(1)、已知凸五边形ABCDE的各条边都相等①如图1,若AC=AD=BE=BD=CE,求证:五边形ABCDE是正五边形
②2如图2,若AC=BE=CE,请判断五边形ABCDE是不是正五边形,并说明理由
(2)、判断下列命题的真假,(在括号内填写“真”或“假”),如图3,已知凸六边形ABCDEF的各条边都相等①若AC=CE=EA,则六边形ABCDEF是正六边形()
②若AD=BE=CF,则六边形ABCDEF是正六边形()
23. 已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4)(1)、求b,c满足的关系式(2)、设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式(3)、若该函数的图象不经过第三象限,当-5sx≤1时,函数的最大值与最小值之差为16,求b的值24. 如图,正方形ABCD的边长为2,E为AB的中点,P是BA延长线上的一点,连接PC交AD于点F,AP=FD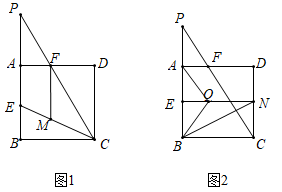 (1)、求 的值(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.
(1)、求 的值(2)、如图1,连接EC,在线段EC上取一点M,使EM=EB,连接MF,求证MF=PF;(3)、如图2,过点E作EN⊥CD于点N,在线段EN上取一点Q,使AQ=AP,连接BQ,BN.将△AQB绕点A旋转,使点Q旋转后的对应点Q'落在边AD上.请判断点B旋转后的对应点B'是否落在线段BN上,并说明理由.