2016-2017学年江苏省盐城市东台市第六教育联盟八年级下学期期中数学试卷
试卷更新日期:2017-05-31 类型:期中考试
一、选择题
-
1. 把分式 中的x和y都扩大3倍,分式的值( )A、不变 B、扩大3倍 C、缩小3倍 D、扩大9倍2. 下列约分结果正确的是( )A、 B、 =x﹣y C、 =﹣m+1 D、3. 四张质地、大小、背面完全相同的卡片上,正面分别画有圆、矩形、等边三角形、等腰梯形四个图案.现把它们的正面向下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案是中心对称图形的概率为( )A、 B、 C、 D、14. 函数y= 的图象与直线y=x有交点,那么k的取值范围是( )A、k>1 B、k<1 C、k>﹣1 D、k<﹣15. 正方形具有而矩形不具有的性质是( )A、对角线互相平分 B、对角线相等 C、对角线互相平分且相等 D、对角线互相垂直6. 小明乘出租车去体育场,有两条路线可供选择:路线一的全程是25千米,但交通比较拥堵,路线二的全程是30千米,平均车速比走路线一时的平均车速能提高80%,因此能比走路线一少用10分钟到达.若设走路线一时的平均速度为x千米/小时,根据题意,得( )A、 B、 C、 D、7. 若顺次连接一个四边形的各边的中点所得的四边形是矩形,则原来的四边形的两条对角线( )A、互相垂直且相等 B、相等 C、互相平分且相等 D、互相垂直8. 如图,菱形OABC的顶点C的坐标为(3,4).顶点A在x轴的正半轴上,反比例函数y= (x>0)的图象经过顶点B,则k的值为( )
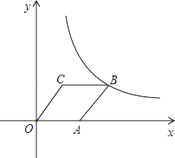 A、12 B、20 C、24 D、329. 小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:
A、12 B、20 C、24 D、329. 小明在学习了正方形之后,给同桌小文出了错题,从下列四个条件:①AB=BC,
②∠ABC=90°,
③AC=BD,
④AC⊥BD
中选两个作为补充条件,使▱ABCD为正方形(如图所示),现有如下四种选法,你认为其中错误的是( )
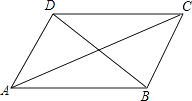 A、①② B、①③ C、②③ D、②④
A、①② B、①③ C、②③ D、②④二、填空题
-
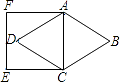
10. 已知:如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为 .
 11. 当x=时,分式 的值为零.12. 矩形的两条对角线的夹角为60°,较短的边长为2cm,则较长的边长为cm.13. 如图,在▱ABCD中,∠BAD的平分线AE交边CD于点E,AB=5cm,BC=3cm,则EC=cm.
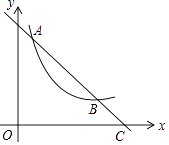
11. 当x=时,分式 的值为零.12. 矩形的两条对角线的夹角为60°,较短的边长为2cm,则较长的边长为cm.13. 如图,在▱ABCD中,∠BAD的平分线AE交边CD于点E,AB=5cm,BC=3cm,则EC=cm.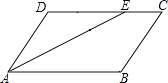 14. 反比例函数y= 的图象经过点(2,﹣1),则k的值为 .15. ÷ 的运算结果是 .16. 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,直角边AB=6,反比例函数y= (x>0)的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .
14. 反比例函数y= 的图象经过点(2,﹣1),则k的值为 .15. ÷ 的运算结果是 .16. 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,直角边AB=6,反比例函数y= (x>0)的图象经过AO的中点C,且与AB交于点D,则点D的坐标为 .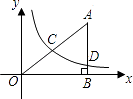
三、解答题
-
17. 根据题意解答(1)、计算: •(2)、解方程: ﹣ =1.18. 如图,直线y=k1x+b(k1≠0)与双曲线y= (k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.
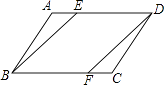
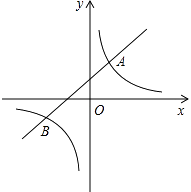 (1)、求直线和双曲线的解析式.(2)、若A1(x1 , y1),A2(x2 , y2),A3(x3 , y3)为双曲线上的三点,且x1<x2<0<x3 , 请直接写出y1 , y2 , y3的大小关系式.19. 如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF.
(1)、求直线和双曲线的解析式.(2)、若A1(x1 , y1),A2(x2 , y2),A3(x3 , y3)为双曲线上的三点,且x1<x2<0<x3 , 请直接写出y1 , y2 , y3的大小关系式.19. 如图,在▱ABCD中,点E、F分别在AD、BC上,且AE=CF.求证:四边形BFDE是平行四边形.
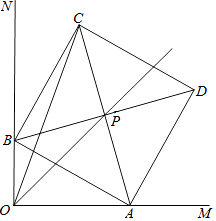
 20. 如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.
20. 如图,在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,AB,CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.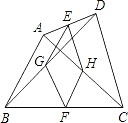 21. 到离学校15千米的风景区去秋游,骑车的同学提前40分钟出发,其余的同学乘汽车出发,结果他们同时到达.已知汽车的速度是自行车的3倍,求自行车和汽车的速度.22. 已知:如图,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.求证:四边形CEDF是正方形.
21. 到离学校15千米的风景区去秋游,骑车的同学提前40分钟出发,其余的同学乘汽车出发,结果他们同时到达.已知汽车的速度是自行车的3倍,求自行车和汽车的速度.22. 已知:如图,在Rt△ABC中,∠C=90°,∠BAC、∠ABC的平分线相交于点D,DE⊥BC,DF⊥AC,垂足分别为E、F.求证:四边形CEDF是正方形.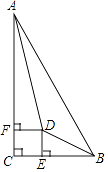 23. 已知y=y1﹣y2 , y1与x2成正比例,y2与x+3成反比例,当x=0时,y=2;当x=2时,y=0,求y与x的函数关系式,并指出自变量的取值范围.24. 病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
23. 已知y=y1﹣y2 , y1与x2成正比例,y2与x+3成反比例,当x=0时,y=2;当x=2时,y=0,求y与x的函数关系式,并指出自变量的取值范围.24. 病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.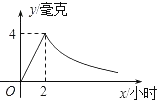 (1)、求当0≤x≤2时,y与x的函数关系式;(2)、求当x>2时,y与x的函数关系式;(3)、若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
(1)、求当0≤x≤2时,y与x的函数关系式;(2)、求当x>2时,y与x的函数关系式;(3)、若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?