2016-2017学年江苏省盐城市东台市第二教育联盟八年级下学期期中数学试卷
试卷更新日期:2017-05-31 类型:期中考试
一、选择题
-
1. 在式子 、 、 、 、 、 中,分式的个数有( )A、2个 B、3个 C、4个 D、5个2. 下列图形中既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 要使得分式 无意义,则x的取值范围为( )A、x>2 B、x≥2 C、x=2 D、x≠24. 若分式 ,则分式 的值等于( )A、﹣ B、 C、﹣ D、5. 反比例函数y= 图象上的两上点为(x1 , y1),(x2 , y2),且x1<x2 , 则下列关系成立的是( )A、y1>y2 B、y1<y2 C、y1=y2 D、不能确定6. 在下列性质中,矩形具有而菱形不一定有的是( )A、对角线互相垂直 B、对角线互相平分 C、四个角是直角 D、四条边相等7. 若方程 =7有增根,则k=( )A、﹣1 B、0 C、1 D、68. 如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( )
3. 要使得分式 无意义,则x的取值范围为( )A、x>2 B、x≥2 C、x=2 D、x≠24. 若分式 ,则分式 的值等于( )A、﹣ B、 C、﹣ D、5. 反比例函数y= 图象上的两上点为(x1 , y1),(x2 , y2),且x1<x2 , 则下列关系成立的是( )A、y1>y2 B、y1<y2 C、y1=y2 D、不能确定6. 在下列性质中,矩形具有而菱形不一定有的是( )A、对角线互相垂直 B、对角线互相平分 C、四个角是直角 D、四条边相等7. 若方程 =7有增根,则k=( )A、﹣1 B、0 C、1 D、68. 如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,则菱形ABCD的周长是( ) A、32 B、24 C、40 D、209. 已知关于x的函数y=k(x﹣1)和y=﹣ (k≠0),它们在同一坐标系内的图象大致是( )A、
A、32 B、24 C、40 D、209. 已知关于x的函数y=k(x﹣1)和y=﹣ (k≠0),它们在同一坐标系内的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
10. 如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )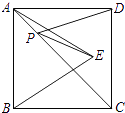 A、 B、3 C、4 D、2
A、 B、3 C、4 D、2二、填空题
-
11. 利用分式的基本性质约分: = .12. 在英语句子“Wish you success!”(祝你成功!)中任选一个字母,这个字母为“s”的概率为 .13. 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=5cm,则EF=cm.
 14. 已知 是反比例函数,那么k的值是 .15. 菱形的两条对角线分别为3cm和4cm,则菱形的面积为cm.16. 如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是 .
14. 已知 是反比例函数,那么k的值是 .15. 菱形的两条对角线分别为3cm和4cm,则菱形的面积为cm.16. 如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是 .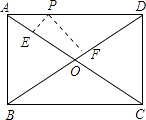 17. 关于x的分式方程 =﹣2解为正数,则m的取值范围是 .18. 如图,在△ABC中,AB=2,AC= ,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 .
17. 关于x的分式方程 =﹣2解为正数,则m的取值范围是 .18. 如图,在△ABC中,AB=2,AC= ,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 .
三、解答题
-
19.
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
①画出△ABC关于原点O的中心对称图形△A1B1C1;
②画出将△ABC绕点C顺时针旋转90°得到△A2B2C.
 20. 计算下列各式.(1)、(2)、 ﹣a﹣1.21. 先化简代数式(1﹣ )÷ ,再从0,﹣2,2,﹣1,1中选取一个恰当的数作为a的值代入求值.22. 解方程:(1)、 +1= ;(2)、 = .23. 如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.
20. 计算下列各式.(1)、(2)、 ﹣a﹣1.21. 先化简代数式(1﹣ )÷ ,再从0,﹣2,2,﹣1,1中选取一个恰当的数作为a的值代入求值.22. 解方程:(1)、 +1= ;(2)、 = .23. 如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F. (1)、求证:四边形ECBF是平行四边形;(2)、当∠A=30°时,求证:四边形ECBF是菱形.24. 如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
(1)、求证:四边形ECBF是平行四边形;(2)、当∠A=30°时,求证:四边形ECBF是菱形.24. 如图,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1. (1)、求点A、B、D的坐标;(2)、求一次函数与反比例函数的解析式;(3)、在x>0的条件下,根据图象说出反比例函数的值大于一次函数值的x的取值范围.25. 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
(1)、求点A、B、D的坐标;(2)、求一次函数与反比例函数的解析式;(3)、在x>0的条件下,根据图象说出反比例函数的值大于一次函数值的x的取值范围.25. 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG. (1)、求证:△CBG≌△CDG;(2)、求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;(3)、连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.
(1)、求证:△CBG≌△CDG;(2)、求∠HCG的度数;并判断线段HG、OH、BG之间的数量关系,说明理由;(3)、连结BD、DA、AE、EB得到四边形AEBD,在旋转过程中,四边形AEBD能否为矩形?如果能,请求出点H的坐标;如果不能,请说明理由.