2016-2017学年江苏省苏州市工业园区八年级下学期期中数学试卷

试卷更新日期：2017-05-31 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各式： $\frac{1}{5}$ （1﹣x）， $\frac{4 x}{π - 3}$ ， $\frac{x^{2} - y^{2}}{2}$ ， $\frac{1 + a}{b}$ ， $\frac{5 x^{2}}{y}$ ，其中分式共有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
2. 下列式子中，y是 $x$ 的反比例函数的是（）

A、 $y = \frac{1}{x^{2}}$ B、 $y = \frac{x}{2}$ C、 $y = \frac{x}{x + 1}$ D、 $x y = 1$

查看试题解析
3. 分式 $\frac{1}{x - 1}$ 有意义，则x的值为（）

A、x=1 B、x≠0 C、x≠1 D、x=0

查看试题解析
4. 在反比例函数 $y = \frac{k - 1}{x}$ 的图象的每一条曲线上，y都随x的增大而减小，则k的取值范围是（）

A、k＞1 B、k＞0 C、k≥1 D、k＜1

查看试题解析
5. 如果把分式 $\frac{3 n}{m - n}$ 中的m和n都扩大3倍，那么分式的值（）

A、不变 B、扩大3倍 C、缩小3倍 D、扩大9倍

查看试题解析
6. 如图，矩形ABCD对角线相交于点O，∠AOB=60°，AB=4，则矩形的边AC为（）

A、4 B、8 C、4 $\sqrt{3}$ D、10

查看试题解析
7. 如图，在菱形ABCD中，∠BAD=120°．已知△ABC的周长是15，则菱形ABCD的周长是（）

A、25 B、20 C、15 D、10

查看试题解析
8. 如图，在平行四边形ABCD中，BD为对角线，点E、O、F分别是 AB、BD、BC的中点，且OE=3，OF=2，则平行四边形ABCD的周长为（）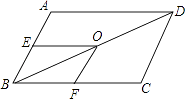

A、10 B、12 C、15 D、20

查看试题解析
9. 如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= $\frac{6}{x}$ 在第一象限的图象经过点B，则△OAC与△BAD的面积之差S_△_OAC﹣S_△_BAD为（）

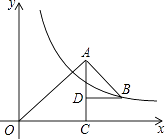A、36 B、12 C、6 D、3

查看试题解析
10. 如图，在正方形OABC中，点B的坐标是（4，4），点E、F分别在边BC、BA上，OE=2 $\sqrt{5}$ ．若∠EOF=45°，则F点的纵坐标是（）

A、 $\frac{4}{3}$ B、1 C、 $\sqrt{2}$ D、 $\sqrt{5}$ ﹣1

查看试题解析

二、填空题

11. 当x=时，分式 $\frac{x + 1}{x - 2}$ 的值为0．

查看试题解析
12. ▱ABCD中，∠A+∠C=100゜，则∠B= ．

查看试题解析
13. 若点（﹣1，2）在双曲线y= $\frac{k}{x}$ （k≠0）上，则此双曲线的函数表达式为．

查看试题解析
14. 约分：① $\frac{5 a b}{20 a^{2} b}$ = ， ② $\frac{x^{2} - 9}{x^{2} - 6 x + 9}$ = ．

查看试题解析
15. 若分式方程 $\frac{x}{x - 4}$ =5+ $\frac{a}{x - 4}$ 有增根，则a的值为．

查看试题解析
16. 如图，双曲线 $y = \frac{k}{x} (k \neq 0)$ 上有一点A，过点A作AB⊥x轴于点B，△AOB的面积为2，则该双曲线的表达式为．

查看试题解析
17.
正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图的方式放置．点A₁ ， A₂ ， A₃ ， …和点C₁ ， C₂ ， C₃ ， …分别在直线y=x+1和x轴上，则点B_n的坐标是．

查看试题解析
18. 如图，在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2015次，点B的落点依次为B₁ ， B₂ ， B₃ ， …，则B₂₀₁₅的坐标为．

查看试题解析

三、解答题

19. 计算下列各式：

(1)、 $\frac{1}{a + 2}$ ﹣ $\frac{4}{4 - a^{2}}$

(2)、 $\frac{x^{2} - 1}{x}$ • $\frac{x}{x + 1}$ +（3x+1）

查看试题解析
20. 解方程：

(1)、 $\frac{x}{x + 3}$ + $\frac{2}{x}$ =1

(2)、 $\frac{2}{3}$ + $\frac{x}{3 x - 1}$ = $\frac{1}{9 x - 3}$ ．

查看试题解析
21. 先化简，再求值： $[1 + \frac{2 x - 4}{(x + 1) (x - 2)}] \div \frac{x + 3}{x^{2} - 1}$ ，其中x=6．

查看试题解析
22. 如图，在△ABC中，AB=AC，D为边BC上一点，以AB、BD为邻边作平行四边形ABDE，连接AD、EC．若BD=CD，求证：四边形ADCE是矩形．

查看试题解析
23. 如图是函数y= $\frac{3}{x}$ 与函数y= $\frac{6}{x}$ 在第一象限内的图象，点P是y= $\frac{6}{x}$ 的图象上一动点，PA⊥x轴于点A，交y= $\frac{3}{x}$ 的图象于点C，PB⊥y轴于点B，交y= $\frac{3}{x}$ 的图象于点D．

(1)、求证：D是BP的中点；

(2)、求四边形ODPC的面积．

查看试题解析
24. 某车队要把4000吨货物运到雅安地震灾区（方案定后，每天的运量不变）．

(1)、从运输开始，每天运输的货物吨数n（单位：吨）与运输时间t（单位：天）之间有怎样的函数关系式？

(2)、因地震，到灾区的道路受阻，实际每天比原计划少运20%，则推迟1天完成任务，求原计划完成任务的天数．

查看试题解析
25. 请按要求，只用无刻度的直尺作图（请保留画图痕迹，不写作法）如图，已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是平行四边形，在图中画出∠AOB的平分线．

查看试题解析
26.
如图，在平面直角坐标系中，正比例函数y=kx（k＞0）与反比例函数y= $\frac{3}{x}$ 的图象分别交于A、C两点，已知点B与点D关于坐标原点O成中心对称，且点B的坐标为（m，0）．其中m＞0．

(1)、四边形ABCD的是．（填写四边形ABCD的形状）

(2)、当点A的坐标为（n，3）时，四边形ABCD是矩形，求m，n的值．

(3)、试探究：随着k与m的变化，四边形ABCD能不能成为菱形？若能，请直接写出k的值；若不能，请说明理由．

查看试题解析
27.
如图，在Rt△ABC中，∠BAC=90°，AB＞AC，射线AM平分∠BAC．

(1)、设AM交BC于点D，DE⊥AB于点E，DF⊥AC于点F，连接EF．有以下三种“判断”：
判断1：AD垂直平分EF．
判断2：EF垂直平分AD．
判断3：AD与EF互相垂直平分．
你同意哪个“判断”？简述理由；

(2)、若射线AM上有一点N到△ABC的顶点B，C的距离相等，连接NB，NC．
①请指出△NBC的形状，并说明理由；
②当AB=11，AC=7时，求四边形ABNC的面积．

查看试题解析