浙江省杭州市2019年中考数学试卷
试卷更新日期:2019-06-21 类型:中考真卷
一、选择题:本大题有10个小题,每小题3分,共30分。
-
1. 计算下列各式,值最小的是( )A、2×0+1-9 B、2+0×1-9 C、2+0-1×9 D、2+0+1-92. 在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )A、m=3,n=2 B、m=-3,n=2 C、m=3,n=2 B.m=-2,n=33. 如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点,若PA=3,则PB=( )
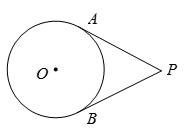 A、2 B、3 C、4 D、54. 已知九年级某班30位学生种树72株,男生每人种3棵树,女生每人种2棵树.设男生有x人,则( )
A、2 B、3 C、4 D、54. 已知九年级某班30位学生种树72株,男生每人种3棵树,女生每人种2棵树.设男生有x人,则( )
A、2x+3(72-x)=30 B、3x+2(72-x)=30 C、2x+3(30-x)=72 D、3x+2(30-x)=725. 点点同学对数据26,36,36,46,5■,52进行统计分析,发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、标准差6. 如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B、C重合),连接AM交DE于点N,则( )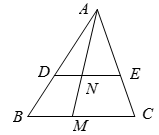 A、 B、 C、 D、7. 在△ABC中,若一个内角等于另两个内角的差,则( )A、必有一个内角等于30° B、必有一个内角等于45° C、必有一个内角等于60° D、必有一个内角等于90°8. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、
A、 B、 C、 D、7. 在△ABC中,若一个内角等于另两个内角的差,则( )A、必有一个内角等于30° B、必有一个内角等于45° C、必有一个内角等于60° D、必有一个内角等于90°8. 已知一次函数y1=ax+b和y2=bx+a(a≠b),函数y1和y2的图象可能是( )A、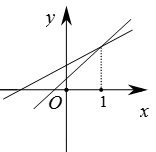 B、
B、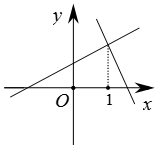 C、
C、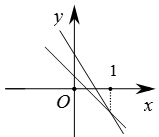 D、
D、 9. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
9. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )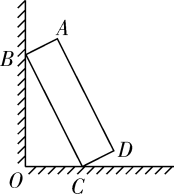 A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx10. 在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )A、M=N-1或M=N+1 B、M=N-1或M=N+2 C、M=N或M=N+1 D、M=N或M=N-1
A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx10. 在平面直角坐标系中,已知a≠b,设函数y=(x+a)(x+b)的图象与x轴有M个交点,函数y=(ax+1)(bx+1)的图象与x轴有N个交点,则( )A、M=N-1或M=N+1 B、M=N-1或M=N+2 C、M=N或M=N+1 D、M=N或M=N-1二、填空题:本大题有6个小题,每小题4分,共24分,
-
11. 因式分解:1-x2=.12. 某计算机程序第一次算得m个数据的平均数为x,第二次算得另外n个数据的平均数为y,则这m+n个数据的平均数等于。13. 如图是一个圆锥形冰淇淋外壳(不计厚度).已知其母线长为12cm,底面圆半径为3cm,则这个冰淇淋外壳的侧面积等于cm2(结果精确到个位).
 14. 在直角三角形ABC中,若2AB=AC,则cosC=.15. 某函数满足当自变量x=1时,函数值y=0;当自变量x=0时,函数值y=1.写出一个满足条件的函数表达式.16. 如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A'点,D点的对称点为D'点,若∠FPG=90°,△A'EP的面积为4,△D'PH的面积为1.则矩形ABCD的面积等于。
14. 在直角三角形ABC中,若2AB=AC,则cosC=.15. 某函数满足当自变量x=1时,函数值y=0;当自变量x=0时,函数值y=1.写出一个满足条件的函数表达式.16. 如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A'点,D点的对称点为D'点,若∠FPG=90°,△A'EP的面积为4,△D'PH的面积为1.则矩形ABCD的面积等于。
三、解答题:本大题有7个小题,共66分.
-
17. 化简:
圆圆的解答如下:
=4x-2(x+2)-(x2-4)
=-x2+2x.
圆圈的解答正确吗?如果不正确,写出正确的解答,
18. 称量五筐水果的质量,若每筐以50千克为基准,超过基准部分的千克数记为正数,不足基准部分的千克数记为负数.甲组为实际称量读数,乙组为记录数据。并把所得数据整理成如下统计表和未完成的统计图(单位:千克).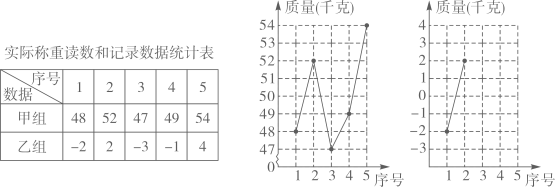 (1)、补充完整乙组数据的折线统计图。
(1)、补充完整乙组数据的折线统计图。
(2)、①甲,乙两组数据的平均数分别为了 , ,写出 与 之间的等量关系.②甲,乙两组数据的方差分别为S甲2 , S乙2 , 比较S甲2与S乙2的大小,并说明理由.
19. 如图,在△ABC中,AC<AB<BC.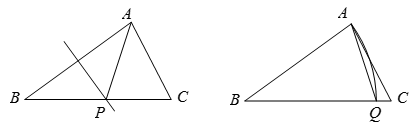 (1)、已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)、以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.20. 方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为(单位:千米/小时),且全程速度限定为不超过120千米/小时。(1)、求v关于t的函数表达式。(2)、方方上午8点驾驶小汽车从A地出发.
(1)、已知线段AB的垂直平分线与BC边交于点P,连接AP,求证:∠APC=2∠B.(2)、以点B为圆心,线段AB的长为半径画弧,与BC边交于点Q.连接AQ若∠AQC=3∠B,求∠B的度数.20. 方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间为t(单位:小时),行驶速度为(单位:千米/小时),且全程速度限定为不超过120千米/小时。(1)、求v关于t的函数表达式。(2)、方方上午8点驾驶小汽车从A地出发.①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶速度v的范围.
②方方能否在当天11点30分前到达B地?说明理由
21. 如图,已知正方形ABCD的边长为1,正方形CEFG的面积为S1 , 点E在DC边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为 S2 , 且S1=S2. (1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.22. 设二次函数y=(x-x1)(x-x2)(x1 , x2是实数)。(1)、甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x= 时,y=- ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)、写出二次函数图象的对称轴,并求该函数的最小值(用含x1 , x2的代数式表示).(3)、已知二次函数的图象经过(0,m)和(1,n)两点(m.n是实数)当0<x1<x2<1时,求证:0<mn< .23. 如图,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D,连接OA.
(1)、求线段CE的长.(2)、若点日为BC边的中点,连接HD,求证:HD=HG.22. 设二次函数y=(x-x1)(x-x2)(x1 , x2是实数)。(1)、甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x= 时,y=- ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)、写出二次函数图象的对称轴,并求该函数的最小值(用含x1 , x2的代数式表示).(3)、已知二次函数的图象经过(0,m)和(1,n)两点(m.n是实数)当0<x1<x2<1时,求证:0<mn< .23. 如图,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D,连接OA.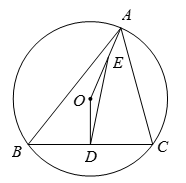 (1)、若∠BAC=60°,
(1)、若∠BAC=60°,①求证:OD= OA.
②当OA=1时,求△ABC面积的最大值。
(2)、点E在线段OA上,(OE=OD.连接DE,设∠ABC=m∠OED.∠ACB=n∠OED(m,n是正数).若∠ABC<∠ACB,求证:m-n+2=0.