2016-2017学年湖北省孝感市云梦县七年级下学期期中数学试卷
试卷更新日期：2017-05-31 类型：期中考试
一、选择题
-
1. ﹣8的立方根是（ ）A、﹣2 B、±2 C、﹣4 D、±42. 如图，∠1和∠2是对顶角的是（ ）A、
B、
C、
D、
3. 若|a|= ，则a=（ ）A、 B、﹣ C、± D、34. 在平面直角坐标系中，点P（﹣2，x2+1）所在的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如图，a∥b，∠1=72°，∠3=63°，则∠2的度数是（ ）
A、45° B、62° C、63° D、72°6. 下列说法错误的是（ ）A、1的平方根是±1 B、2是8的立方根 C、 是2的一个平方根 D、﹣3是 的平方根7. 如图，想在河堤两岸搭建一座桥，图中搭建方式中，最短的是（ ）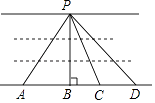
A、PA B、PB C、PC D、PD8. 如图，直线a，b被直线c所截，下列条件能使a∥b的是（ ）
A、∠1=∠3 B、∠2=∠5 C、∠3=∠6 D、∠4=∠89.如图，三角形ABC中任意一点P（x0 ， y0）经平移后对应点为P1（x0+3，y0﹣1），将三角形ABC作同样的平移得到三角形A1B1C1 ， 则A1的坐标是（ ）
A、（﹣4，3） B、（﹣4，5） C、（2，3） D、（2，5）10. 以下五个命题：①对顶角相等；②内错角相等；③同位角相等，两直线平行；④0的立方根是0；⑤无限不循环小数是无理数．其中真命题的个数为（ ）A、2 B、3 C、4 D、5二、填空题
-
11. 1﹣ 的相反数是 ．12. 已知（x﹣2）2=1，则x= ．13. 如图，边长为4cm的正方形ABCD先向左平移1cm，再向上平移2cm，得到正方形A′B′C′D′，则两正方形公共部分的面积为 cm2 ．
14. 如图，直线AB∥CD，AC⊥BC于点C，若∠1=44°，则∠2的度数是 ．
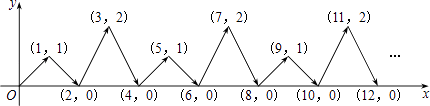
15. 比较大小： ﹣3（填“＞”、“=”或“＜”）16.如图，动点P在平面直角坐标系中按图中箭头所示的方向运动，第1次从原点运动到（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过2017次运动后，动点P的坐标为
三、解答题
-
17. 计算：(1)、 （ ﹣1）(2)、| ﹣ |+2(3)、 + ．18. 如图，AB⊥CD，垂足为O，直线EF经过点O．
(1)、写出∠1的邻补角；(2)、若∠1=30°，求∠2，∠3，∠4的度数．
19. 正数x的两个平方根分别为3﹣a和2a+7．(1)、求a的值；(2)、求44﹣x这个数的立方根．20. 如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠3=∠4，求证：∠5=∠6．
21. 已知平面直角坐标系内三个点的坐标为A（1，4），B（3，2），O（0，0），求△ABO的面积．22. 在平面直角坐标系内，已知A（2x，3x+1）．(1)、点A在x轴下方，在y轴的左侧，且到两坐标轴的距离相等，求x的值；(2)、若x=1，点B在x轴上，且S△OAB=6，求点B的坐标．23. 如图，直线AB∥CD，∠B=∠D=120°，E，F在AB上，且∠1=∠2，∠3=∠4
(1)、求证：AD∥BC；(2)、求∠ACE的度数；(3)、若平行移动AD，那么∠CAF：∠CFE的值是否发生变化？若变化，找出变化规律或求出其变化范围；若不变，求出这个比值．
24. 课题学习：平行线的“等角转化”功能【阅读理解】如图1，已知点A是BC外一点，连接AB、AC，求∠BAC+∠B∠C的度数．
(1)、阅读并补充下面推理过程．解：过点A作DE∥BC，所以∠B= ， ∠C= ．
又∵∠DAB+∠BAC+∠EAC=180°
∴∠B+∠BAC+∠C=180°
(2)、从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C“凑”在一起，得出角之间的关系，使问题得以解决．(3)、如图2，已知AB∥CD，点C在点D的右侧，∠ADC=50°，BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间，如图3，若∠ABC=n°，求∠BED的度数（用含n的代数式表示）