2016-2017学年湖北省荆州市洪湖市八年级下学期期中数学试卷
试卷更新日期：2017-05-31 类型：期中考试
一、选择题
-
1. 下列根式不是最简二次根式的是（ ）A、 B、 C、 D、2. 下列说法正确的是（ ）A、对角线互相垂直的四边形是菱形 B、矩形的对角线互相垂直 C、四边相等的四边形是菱形 D、一组对边平行的四边形是平行四边形3. △ABC中∠A、∠B、∠C的对边分别是a、b、c，下列命题中的假命题是（ ）A、如果∠C﹣∠B=∠A，则△ABC是直角三角形 B、如果c2=b2﹣a2 ， 则△ABC是直角三角形，且∠C=90° C、如果（c+a）（c﹣a）=b2 ， 则△ABC是直角三角形 D、如果∠A：∠B：∠C=5：2：3，则△ABC是直角三角形4. 直角三角形中，两直角边分别是12和5，则斜边上的中线长是（ ）A、34 B、26 C、8.5 D、6.55. 顺次连结四边形四条边的中点，所得的四边形是矩形，则原四边形一定是（ ）A、平行四边形 B、对角线相等的四边形 C、对角线互相垂直的四边形 D、矩形6. 在联欢会上，有A、B、C三名选手站在一个三角形的三个顶点的位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的最适当的位置是在△ABC的（ ）A、三边中线的交点 B、三边垂直平分线的交点 C、三条角平分线的交点 D、三边上高的交点7.
如图，一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B，则它走过的路程最短为（ ）
A、 a B、（1+ ）a C、3a D、 a8. 矩形的面积为12cm2 ， 周长为14cm，则它的对角线长为（ ）A、5cm B、6cm C、 cm D、 cm9. 下列根式中，与是同类二次根式的是（ ）A、 B、 C、 D、10. 如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（ ）
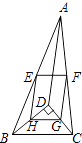A、7 B、9 C、10 D、11二、填空题
-
11. 的平方根为 ．12. 二次根式 有意义的条件是 ．13. 如图，菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，过点O作OH丄AB，垂足为H，则点0到边AB的距离OH= ．
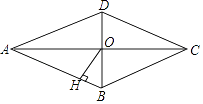14. 计算：（1+ ）2×（1﹣ ）2= ．15. 已知直角三角形两边x、y的长满足|x2﹣4|+ =0，则第三边长为 ．16. 如图，在△ABC中，∠ACB=90°，∠A=30°，AB的垂直平分线分别交AB和AC于点D，E，AE=2，CE= ．
17. 如图，延长矩形ABCD的边BC至点E，使CE=BD，连结AE，如果∠ADB=30°，则∠E=度．
18. 如图△ABC中，点D为BC的中点，AB=5，AC=3，AD=2，则CD长为 ．
三、解答题
-
19. 计算下列各式(1)、 ×（ ﹣π）0+（ ）﹣1(2)、 +（3﹣ ）（1+ ）．20. 先化简，再求值：（ ）÷ ，其中x= ．21. 有10个边长为1的正方形，排列形式如下左图．请在左图中把它们分割，使之拼接成一个大正方形，并把分割后的图形画在右图的正方形网格中．（正方形网格中的每个小正方形边长都是1，每个小格顶点为格点，要求以格点为顶点画大正方形）
22. 如图，在▱ABCD中，O是对角线AC和BD的交点，OE⊥AD于E，OF⊥BC于F．求证：OE=OF．
23. 已知x= ﹣1，y= +1，求代数式x2+xy+y2的值．24. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．
(1)、求证：△ABM≌△DCM；(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；(3)、当AD：AB=时，四边形MENF是正方形（只写结论，不需证明）．25.如图，在▱ABCD中，E、F分别为边AB、CD的中点，BD是对角线，过A点作AG∥DB交CB的延长线于点G．
(1)、求证：DE∥BF；(2)、若∠G=90°，求证：四边形DEBF是菱形；(3)、请利用备用图分析，在（2）的条件下，若BE=4，∠DEB=120°，点M为BF的中点，当点P在BD边上运动时，求PF+PM的最小值，并求出此时线段BP的长．