2016-2017学年湖北省黄石市下陆区八年级下学期期中数学试卷

试卷更新日期：2017-05-31 类型：期中考试

进入出卷网下载

一、选择题

1. 下列式子中，属于最简二次根式的是

A、 $\sqrt{9}$ B、 $\sqrt{7}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2}$ × $\sqrt{3}$ = $\sqrt{6}$ B、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ C、 $\sqrt{8}$ =4 $\sqrt{2}$ D、 $\sqrt{4}$ ﹣ $\sqrt{2}$ = $\sqrt{2}$

查看试题解析
3. 下列说法中错误的是（）

A、平行四边形的对角线互相平分 B、两组对边分别相等的四边形是平行四边形 C、矩形的对角线相等 D、有一组邻边相等且有一个角是直角的四边形是正方形

查看试题解析
4. 已知二条线段的长分别为 $\sqrt{2}$ cm， $\sqrt{3}$ cm，那么能与它们组成直角三角形的第三条线段的长是（）

A、1cm B、 $\sqrt{5}$ cm C、5cm D、1cm与 $\sqrt{5}$ cm

查看试题解析
5.
如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是（　　）

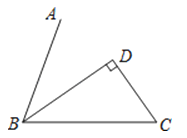A、35° B、55° C、60° D、70°

查看试题解析
6. 如图，△ABC中，AD为BC边上的中线，若AB=5，AC=13，AD=6，那么BC的值为（）

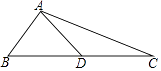A、18 B、 $\sqrt{61}$ C、2 $\sqrt{61}$ D、12

查看试题解析
7. 如图，四边形ABCD为矩形纸片，把纸片ABCD折叠，使点B恰好落在CD边的中点E处，折痕为AF，若CD=6，则AF等于（）

A、 $4 \sqrt{3}$ B、 $3 \sqrt{3}$ C、 $4 \sqrt{2}$ D、8

查看试题解析
8. 如图，△ABC和△DCE都是边长为4的等边三角形，点B、C、E在同一条直线上，连接BD，则BD的长为（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
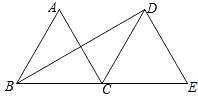9. 如图，△ABC中，M是BC中点，AD平分∠BAC，BD⊥AD于D，延长交AC于N，若AB=10，AC=16，则MD的长为（）

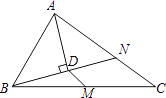A、5 B、4 C、3 D、2

查看试题解析
10. 如图，在平行四边形ABCD中，AB≠AD，对角线AC与BD相交于点O，OE⊥BD交AD于E，若△ABE的周长为12cm，则平行四边形ABCD的周长是（）

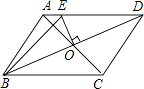A、40cm B、24cm C、48cm D、无法确定

查看试题解析

二、填空题

11. 若使 $\sqrt{x + 1}$ 有意义，则x的取值范围是．

查看试题解析
12. 已知 $\sqrt{x - 2} + \sqrt{y + 5}$ =0，则x= ， y= ．

查看试题解析
13. 命题“菱形是对角线互相垂直的四边形”的逆命题是．

查看试题解析
14. 如图，将边长都为2 $\sqrt{2}$ cm的正方形按如图所示摆放，点A₁、A₂、…、A_n分别是正方形的中心，则2014个这样的正方形重叠部分的面积和为．

查看试题解析
15. 直角三角形ABCD中，∠BAC=90°，AB=AC=1，以AC为一边在△ABC外部作等腰直角三角形ACD，则线段BD的长为．

查看试题解析
16. 如图，在等边△ABC中，AB=4，P、M、N分别是BC、CA、AB边上动点，则PM+MN的最小值是．

查看试题解析

三、解答题

17. （ $\frac{1}{2}$ ）^﹣²﹣|2 $\sqrt{2}$ ﹣3|﹣（2011﹣π）⁰+ $\frac{3}{\sqrt{8}}$ ．

查看试题解析
18. 已知 $x = \sqrt{3} + \sqrt{2}$ 和 $y = \sqrt{3} - \sqrt{2}$ ，求下列各式的值：

(1)、x²﹣y²

(2)、x²+2xy+y² ．

查看试题解析
19. 解方程组 ${\begin{array}{l} \sqrt{2} x + y = 2 \\ 4 x - \sqrt{2} y = \sqrt{2} \end{array}$ ．

查看试题解析
20. 如图，四边形ABCD中，∠B=90°，AB=BC=3 $\sqrt{2}$ ，CD=8，AD=10．

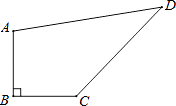(1)、求∠BCD的度数．

(2)、求四边形ABCD的面积．

查看试题解析
21. 如图，E、F是四边形ABCD的对角线BD上的两点，BF=DE，AE=CF，∠1=∠2．

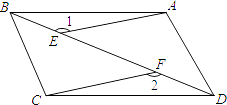(1)、求证：△ABE≌△CDF；

(2)、四边形ABCD是平行四边形吗？请说明理由．

查看试题解析
22. 如图所示是10×8的网格，网格中每个小正方形的边长均为1，A、B两点在小正方形的顶点上，使以A、B、C为顶点的三角形分别满足以下要求：

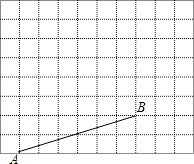(1)、请在图中取一点C（点C必须在小正方形的顶点上），使△ABC为钝角等腰三角形；

(2)、通过计算，直接写出△ABC的周长．

查看试题解析
23.
如图，在一次数学课外活动中，小明同学在点P处测得教学楼A位于北偏东60°方向，办公楼B位于南偏东45°方向．小明沿正东方向前进60米到达C处，此时测得教学楼A恰好位于正北方向，办公楼B正好位于正南方向．求教学楼A与办公楼B之间的距离（结果精确到0.1米）．（供选用的数据： $\sqrt{2}$ ≈1.414， $\sqrt{3}$ ≈1.732）

查看试题解析
24. 观察、思考、解答：
（ $\sqrt{2}$ ﹣1）²=（ $\sqrt{2}$ ）²﹣2×1× $\sqrt{2}$ +1²=2﹣2 $\sqrt{2}$ +1=3﹣2 $\sqrt{2}$
反之3﹣2 $\sqrt{2}$ =2﹣2 $\sqrt{2}$ +1=（ $\sqrt{2}$ ﹣1）²
∴3﹣2 $\sqrt{2}$ =（ $\sqrt{2}$ ﹣1）²
∴ $\sqrt{3 - 2 \sqrt{2}}$ = $\sqrt{2}$ ﹣1

(1)、仿上例，化简： $\sqrt{6 - 2 \sqrt{5}}$ ；

(2)、若 $\sqrt{a + 2 \sqrt{b}} = \sqrt{m} + \sqrt{n}$ ，则m、n与a、b的关系是什么？并说明理由；

(3)、已知x= $\sqrt{4 - \sqrt{12}}$ ，求（ $\frac{1}{x - 2} + \frac{1}{x + 2}$ ）• $\frac{x^{2} - 4}{2 (x - 1)}$ 的值（结果保留根号）

查看试题解析
25.
如图甲，在△ABC中，∠ACB为锐角，点D为射线BC上一动点，连接AD，以AD为一边且在AD的右侧作正方形ADEF，解答下列问题：

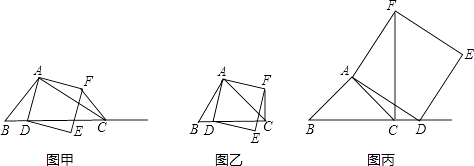(1)、如果AB=AC，∠BAC=90°．
①当点D在线段BC上时（与点B不重合），如图乙，线段CF、BD之间的位置关系是什么？写出它们之间的数量关系．
②当点D在线段BC的延长线上时，如图丙，①中的结论是否仍然成立，请证明？

(2)、如果AB≠AC，∠BAC≠90°，点D在线段BC上运动．试探究：当△ABC满足一个什么条件时，CF⊥BC（点C、F重合除外）？直接写出条件，不需要证明．

(3)、若AC=4 $\sqrt{2}$ ，BC=3，在（2）的条件下，求△ABC中AB边上的高．

查看试题解析