2016-2017学年河南省濮阳市濮阳县十校八年级下学期期中数学试卷
试卷更新日期：2017-05-31 类型：期中考试
一、选择题
-
1. 若式子 有意义，则x的取值范围为（ ）A、x≥2 B、x≠3 C、x≥2或x≠3 D、x≥2且x≠32. 下列计算不正确的是（ ）A、 ﹣ = B、3 ×2 =6 C、（2 ）2=8 D、 =3. 在四边形ABCD中，从①AB∥CD；②AB=CD；③BC∥AD；④BC=AD中任选两个使四边形ABCD为平行四边形的选法有（ ）A、3 B、4 C、5 D、64. 已知x、y为正数，且|x﹣4|+（y﹣3）2=0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为直径的圆的面积为（ ）A、5π B、25π C、7π D、6.25π5. 已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）A、当AB=BC时，它是菱形 B、当AC=BD时，它是正方形 C、当AC⊥BD时，它是菱形 D、当∠ABC=90°时，它是矩形6. 将五个边长都为3cm的正方形按如图所示摆放，点A、B、C、D分别是四个正方形的中心，则图中四块阴影面积的和为（ ）
A、3cm2 B、6cm2 C、9cm2 D、18cm27. 如图，菱形ABCD中对角线相交于点O，且OE⊥AB，若AC=16，BD=12，则OE的长是（ ）
A、5 B、10 C、4.8 D、不确定8. 如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：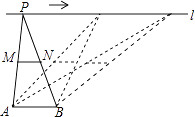
①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．
其中会随点P的移动而变化的是（ ）
A、②③ B、②⑤ C、①③④ D、④⑤二、填空题
-
9. 若整数x满足|x|≤3，则使 为整数的x的值是（只需填一个）．10. 如图所示，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却踩伤了花草．
11. 计算 的结果是 ．12. 如图，在▱ABCD中，BE⊥AB交对角线AC于点E，若∠2的度数为110°，则∠1= ．
13. 如图，在△ABC中，CA=CB，AD⊥BC，BE⊥AC，AB=5，AD=4，则AE= ．
14. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB=90°，若AB=16，BC=18，则EF的长为 ．
15. 如图，▱ABCD中，∠ABC=60°，点E、F分别在CD和BC的延长线上，AE∥BD，EF⊥BC，AB的长是1，则EF= ．
三、解答题
-
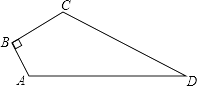
16. 计算：﹣2﹣2÷|﹣ |+ ﹣（π﹣6）0 ．17. 计算： ．18. 如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．
19. 如图，在△ABC中，AD⊥BC，垂足为D，∠B=60°，∠C=45°．
(1)、求∠BAC的度数．(2)、若AC=2，求AB的长．20. 如图，在平行四边形ABCD中，E、F是对角线BD上的两点，且BF=DE．求证：AE∥CF．
21. 如图，四边形ABCD中，AD∥BC，BA⊥AD，BC=DC，BE⊥CD于点E．
(1)、求证：△ABD≌△EBD；(2)、过点E作EF∥DA，交BD于点F，连接AF．求证：四边形AFED是菱形．22. 如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点．点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD、AN．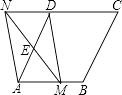
(1)、求证：四边形AMDN是平行四边形；(2)、填空：①当AM的值为时，四边形AMDN是矩形；②当AM的值为时，四边形AMDN是菱形．
23. 如图，点E是矩形ABCD的对角线BD上的一点，且BE=BC，AB=3，BC=4，点P为直线EC上的一点，且PQ⊥BC于点Q，PR⊥BD于点R．
(1)、①如图1，当点P为线段EC中点时，易证：PR+PQ= （不需证明）．②如图2，当点P为线段EC上的任意一点（不与点E、点C重合）时，其它条件不变，则①中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由．
(2)、如图3，当点P为线段EC延长线上的任意一点时，其它条件不变，则PR与PQ之间又具有怎样的数量关系？请直接写出你的猜想．