2016-2017学年江苏省苏州市工业园区七年级下学期期中数学试卷
试卷更新日期：2017-05-31 类型：期中考试
一、选择题
-
1. 计算（﹣4）2×0.252的结果是（ ）A、1 B、﹣1 C、﹣ D、2. 下列分解因式正确的是（ ）A、x3﹣x=x（x2﹣1） B、m2+m﹣6=（m+3）（m﹣2） C、（a+4）（a﹣4）=a2﹣16 D、x2+y2=（x+y）（x﹣y）3. 若一个多边形的每个内角都为135°，则它的边数为（ ）A、6 B、8 C、5 D、104. 在△ABC中，∠A= ∠B= ∠C，则△ABC是（ ）A、钝角三角形 B、直角三角形 C、锐角三角形 D、无法确定5. 如果a=（﹣0.1）0 ， b=（﹣0.1）﹣1 ， c=（﹣ ）﹣2 ， 那么a，b，c的大小关系为（ ）A、a＞b＞c B、c＞a＞b C、c＞b＞a D、a＞c＞b6. 设A=（x﹣3）（x﹣7），B=（x﹣2）（x﹣8），则A、B的大小关系为（ ）A、A＞B B、A＜B C、A=B D、无法确定7. 如图，DE∥BC，EF∥AB，图中与∠BFE互补的角共（ ）个．
A、2个 B、3个 C、4个 D、5个8. 如图，把一块含45°角的三角板的直角顶点靠在长尺（两边a∥b）的一边b上，若∠1=30°，则三角板的斜边与长尺的另一边a的夹角∠2的度数为（ ）
A、10° B、15° C、30° D、35°9. 如图，在五边形ABCDE中，∠A+∠B+∠E=α，DP、CP分别平分∠EDC、∠BCD，则∠P的度数是（ ）
A、 α﹣90° B、90° C、 D、540°二、填空题
-
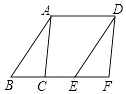
10. 一个等腰三角形的两边长分别为3和7，这个三角形的周长是 ．11. 若a﹣b=1，则 （a2+b2）﹣ab﹦ ．12. 若（2a﹣3b）2=（2a+3b）2+N，则表示N的代数式是 ．13. 如果（x+1）（x2﹣4ax+a）的乘积中不含x2项，则a为 ．14. 如图，面积为8cm2的△ABC沿BC方向平移至△DEF位置，平移的距离是边BC长的两倍，则图中四边形ACED的面积是 cm2 ．
15. 当x=2017时，代数式（x﹣1）（3x+2）﹣3x（x+3）+10x的值为 ．16. 将正三角形、正四边形、正五边形按如图所示的位置摆放．如果∠3=30°，那么∠1+∠2=°．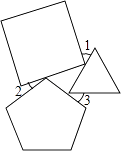
17. 如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积 ．
三、解答题
-
18. 计算(1)、|﹣ |+（π﹣3）0+（﹣ ）3﹣（ ）﹣2(2)、（﹣x2）3+3x2•x4﹣（﹣2x3）•x3 ．19. 分解因式(1)、x3﹣xy2(2)、（x+2）（x+4）+1．20.
已知：如图，AB∥CD，∠A=∠D．求证：AF∥ED．
21. 综合题。(1)、将△ABC向下平移1个单位，向右平移7个单位，在给定方格纸中画出平移后的△A′B′C′；画出AB边上的中线CD；画出BC边上的高线AE；(2)、△A′B′C′的面积为 ．(3)、在右图中能使S△PAC=S△ABC的格点P的个数有个（点P异于B）
22. 先化简，再求值：（x+y+2）（x+y﹣2）﹣（x+2y）2+3y2 ， 其中x=﹣ ，y= ．23. 已知3×9m×27m=317+m ， 求：（﹣m2）3÷（m3•m2）的值．24. 阅读下列文字：我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式．例如由图1可以得到（a+2b）（a+b）=a2+3ab+2b2 ．
请解答下列问题：
(1)、写出图2中所表示的数学等式；(2)、利用（1）中所得到的结论，解决下面的问题：已知a+b+c=12，ab+bc+ac=42，求a2+b2+c2的值；(3)、图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片，请利用所给的纸片拼出一个几何图形，使得用两种不同的方法计算它的面积时，能够得到数学公式：2a2+7ab+3b2=（a+3b）（2a+b）．25. △ABC中，三个内角的平分线交于点O，过点O作OD⊥OB，交边BC于点D．(1)、如图1，猜想∠AOC与∠ODC的关系，并说明你的理由；(2)、如图2，作∠ABC外角∠ABE的平分线交CO的延长线于点F．①求证：BF∥OD；
②若∠F=35°，求∠BAC的度数．
26. 已知，如图，在△ABC中，AE是角平分线，D是AB上的点，AE、CD相交于点F．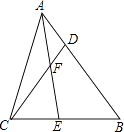
(1)、若∠ACB=∠CDB=90°，求证：∠CFE=∠CEF；(2)、若∠ACB=∠CDB=m（0°＜m＜180°）．①求∠CEF﹣∠CFE的值（用含m的代数式表示）；
②是否存在m，使∠CEF小于∠CFE，如果存在，求出m的范围，如果不存在，请说明理由．