2016-2017学年河北省唐山市路北区八年级下学期期中数学试卷

试卷更新日期：2017-05-31 类型：期中考试

进入出卷网下载

一、选择题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 如图，在平行四边形ABCD中，∠A=40°，则∠C大小为（）

A、40° B、80° C、140° D、180°

查看试题解析
3. 如图，矩形ABCD的对角线AC=8cm，∠AOD=120°，则AB的长为（）

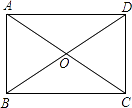A、 $\sqrt{3}$ cm B、2cm C、2 $\sqrt{3}$ cm D、4cm

查看试题解析
4. 下列长度的三条线段能组成直角三角形的是（）

A、4，5，6 B、2，3，4 C、1，1， $\sqrt{2}$ D、1，2，2

查看试题解析
5. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

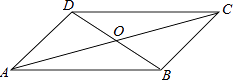A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
6. 矩形、菱形、正方形都具有的性质是（）．

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角

查看试题解析
7.
如图，长为8cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3cm至D点，则橡皮筋被拉长了（　　）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
8. 如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，∠ABC的平分线交AD于点F．若BF=12，AB=10，则AE的长为（）

A、10 B、12 C、16 D、18

查看试题解析
9. 如图为正三角形ABC与正方形DEFG的重叠情形，其中D、E两点分别在AB、BC上，且BD=BE．若AC=18，GF=6，则F点到AC的距离为何？（）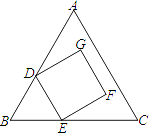

A、2 B、3 C、12﹣4 $\sqrt{3}$ D、6 $\sqrt{3}$ ﹣6

查看试题解析
10. 为了调查某小区居民的用水情况，随机抽查了若干户家庭的月用水量，结果如下表：
月用水量（吨）
3
4
5
8
户数
2
3
4
1
则关于这若干户家庭的月用水量，下列说法错误的是（）

A、众数是4 B、平均数是4.6 C、调查了10户家庭的月用水量 D、中位数是4.5

查看试题解析
11. 甲、乙、丙、丁四位同学最近五次数学成绩统计如表，如果从这四位同学中，选出一位成绩较好且状态稳定的同学参加即将举行的中学生数学竞赛，那么应选（）
甲
乙
丙
丁
平均数
80
85
85
80
方差
42
42
54
59

A、甲 B、乙 C、丙 D、丁

查看试题解析
12. 在△ABC中，AB=15，AC=13，高AD=12，则△ABC中BC边的长为（）

A、9 B、5 C、14 D、4或14

查看试题解析
13. 如图，直线l过正方形ABCD的顶点B，点A、C至直线l的距离分别为2和3，则此正方形的面积为（）

A、5 B、6 C、9 D、13

查看试题解析
14. 如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，点D落在D′处，则重叠部分△AFC的面积是（）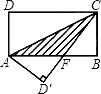

A、8 B、10 C、20 D、32

查看试题解析

二、填空题

15. 如图，平行四形ABCD中，∠A=100°，则∠B+∠D的度数是．

查看试题解析
16. 若直角三角形的两直角边的长分别为a、b，且满足 $\sqrt{a - 3}$ +（b﹣4）²=0，则该直角三角形的斜边长为．

查看试题解析
17. 某中学规定学生的学期体育总评成绩满分为100分，其中平均成绩占20%，期中考试成绩占30%，期末考试成绩占50%，小彤的三项成绩（百分制）依次为95，90，88，则小彤这学期的体育总评成绩为．

查看试题解析
18. 如图，每个小正方形的边长为1，在△ABC中，点D为AB的中点，则线段CD的长为．

查看试题解析

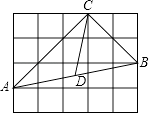
三、解答题

19. 在校园歌手大奖赛上，比赛规则为七位评委打分，去掉一个最高分和一个最低分后，所剩数据取平均数即为选手的最后得分，七位评委给某位歌手打出的分数如下：9.5，9.4，9.6，9.9，9.3，9.7，9.0，则这位歌手的最后得分是多少？

查看试题解析
20. 如图，要从电线杆离地面4m处向地面拉一条钢索，若地面钢索固定点A到电线杆底部B的距离为2m，求钢索的长度．

查看试题解析
21. 如图，在▱ABCD中，E、F为对角线BD上的两点，且∠BAE=∠DCF．求证：BE=DF．

查看试题解析
22. 如图，边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3）．

(1)、写出△AOB的面积为；

(2)、点P在x轴上，当PA+PB的值最小时，在图中画出点P，并直接写出PA+PB的最小值为．

查看试题解析
23. 如图，矩形ABCD的对角线AC、BD交于点O，且DE∥AC，CE∥BD．

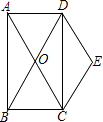(1)、求证：四边形OCED是菱形；

(2)、若∠BAC=30°，AC=4，求菱形OCED的面积．

查看试题解析
24. 为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为A，B，C，D四个等级，其中相应等级的里程依次为200千米，210千米，220千米，230千米，获得如下不完整的统计图．
根据以上信息，解答下列问题：

(1)、问这次被抽检的电动汽车共有几辆？

(2)、补全条形统计图，并求出C等级对应的圆心角度数．

(3)、估计这种电动汽车一次充电后行驶的平均里程数为多少千米？

查看试题解析
25. 如图，在同一平面内，两条平行高速公路l₁和l₂间有一条“Z”型道路连通，其中AB段与高速公路l₁成30°角，长为20km；BC段与AB、CD段都垂直，长为10km，CD段长为30km，求两高速公路间的距离（结果保留根号）．

查看试题解析
26. 如图，在Rt△ABC中，∠ACB=90°，过点C的直线MN∥AB，D为AB边上一点，过点D作DE⊥BC，交直线MN于E，垂足为F，连接CD、BE．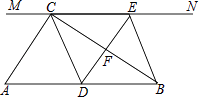

(1)、求证：CE=AD；

(2)、当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由；

(3)、若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的理由．

查看试题解析

月用水量（吨）	3	4	5	8
户数	2	3	4	1

	甲	乙	丙	丁
平均数	80	85	85	80
方差	42	42	54	59