2016-2017学年河北省廊坊市文安县八年级下学期期中数学试卷

试卷更新日期：2017-05-31 类型：期中考试

进入出卷网下载

一、选择题

1. 下列根式不是最简二次根式的是（）

A、 $\sqrt{a^{2} + 1}$ B、 $\sqrt{2 x + 1}$ C、 $\frac{\sqrt{2 b}}{4}$ D、 $\sqrt{0.1 y}$

查看试题解析
2. 正方形的面积是4，则它的对角线长是（　　）

A、2 B、 $\sqrt{2}$ C、2 $\sqrt{2}$ D、4

查看试题解析
3. 能判定四边形ABCD为平行四边形的题设是（）

A、AB∥CD，AD=BC B、AB=CD，AD=BC C、∠A=∠B，∠C=∠D D、AB=AD，CB=CD

查看试题解析
4. 下列计算正确的是（）

A、2 $\sqrt{3}$ +4 $\sqrt{2}$ =6 $\sqrt{5}$ B、 $\sqrt{8}$ =4 $\sqrt{2}$ C、 $\sqrt{27}$ ÷ $\sqrt{3}$ =3 D、 $\sqrt{{(- 3)}^{2}}$ =﹣3

查看试题解析
5. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为（）

A、90° B、60° C、45° D、30°

查看试题解析
6. 矩形具有而一般的平行四边形不一定具有的特征（　　）

A、对角相等 B、对角线相等 C、对角线互相平分 D、对边相等

查看试题解析
7. 若 $\sqrt{3}$ =a， $\sqrt{30}$ =b，则 $\sqrt{0.9}$ =（）

A、 $\frac{a}{10 b}$ B、 $\frac{b}{10 a}$ C、 $\frac{a b}{10}$ D、 $\frac{a + b}{10}$

查看试题解析
8. 已知一个菱形的周长是20cm，两条对角线的比是4：3，则这个菱形的面积是（）

A、12cm² B、24cm² C、48cm² D、96cm²

查看试题解析
9. 直角三角形中，两直角边分别是12和5，则斜边上的中线长是（　　）

A、34 B、26 C、8.5 D、6.5

查看试题解析
10. 如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（）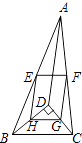

A、7 B、9 C、10 D、11

查看试题解析

二、填空题

11. 若 $\sqrt{2 x - 1}$ 有意义，则x的取值范围是．

查看试题解析
12. 如图，已知OA=OB，那么数轴上点A所表示的数是．

查看试题解析
13. 如图，▱ABCD中，AB的长为8，∠DAB的角平分线交CD于E，若DE：EC=3：1，则BC的长为．

查看试题解析
14. 计算： $\sqrt{3} \div \sqrt{3} \times \frac{1}{\sqrt{3}}$ = ．

查看试题解析
15. 如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为5，则正方形A，B，C，D的面积的和为

查看试题解析
16. 如图，矩形ABCD的对角线相交于点O，AB=4cm，∠AOB=60°，则AC=cm．

查看试题解析
17. 如图，菱形ABCD的边长是4cm，E是AB的中点，且DE⊥AB，则菱形ABCD的面积为cm² ．

查看试题解析
18. 观察下列各式： $\sqrt{1 + \frac{1}{3}}$ =2 $\sqrt{\frac{1}{3}}$ ， $\sqrt{2 + \frac{1}{4}}$ =3 $\sqrt{\frac{1}{4}}$ ， $\sqrt{3 + \frac{1}{5}}$ =4 $\sqrt{\frac{1}{5}}$ ，…请你找出其中规律，并将第n（n≥1）个等式写出来．

查看试题解析

三、解答题

19. 计算下列各式：

(1)、（ $\sqrt{48}$ ﹣4 $\sqrt{\frac{1}{8}}$ ）﹣（3 $\sqrt{\frac{1}{3}}$ ﹣2 $\sqrt{0.5}$ ）

(2)、 $(\sqrt{8} + \sqrt{48}) (\sqrt{2} - \sqrt{12}) - {(\sqrt{2} - \sqrt{3})}^{2}$ ．

查看试题解析
20. 请阅读下列材料：问题：现有5个边长为1的正方形，排列形式如图甲，请把它们分割后拼接成一个新的正方形．要求：画出分割线并在正方形网格图（图中的每一个小正方形的边长均为1）中用实线画出拼接成的新正方形．
小东同学的做法是：设新正方形的边长为x（x＞0），依题意，割补前后图形的面积相等，有x²=5，解得x= $\sqrt{5}$ 由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长．于是，画出如图乙所示的分割线，拼出如图丙所示的新的正方形．
请你参考小东同学的做法，解决如下问题：
现有10个边长为1的小正方形，排列形式如图丁，请把它们分割后拼接成一个新的正方形．要求：在图丁中画出分割线，并在图戊的正方形网格图（图中的每一个小正方形的边长均为1）中用实线画出拼接成的新正方形．
说明：直接画出图形，不要求写分析过程．

查看试题解析
21. 如图，▱ABCD中，点E，F分别在BC，AD上，且AF=CE，求证：AE=CF．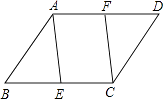

查看试题解析
22. 如图，铁路上A、B两点相距25km，C、D为两村庄，DA⊥AB于A，CB⊥AB于B，已知DA=15km，CB=10km，现在要在铁路AB上建一个土特产品收购站E，使得C、D两村到E站的距离相等，则E站应建在距A站多少千米处？

查看试题解析
23. 如图所示，在矩形ABCD中，对角线AC，BD相交于点O，∠BOC=120°，AC=6，求：

(1)、AB的长；

(2)、矩形ABCD的面积．

查看试题解析
24. 如图，平行四边形ABCD中，AB=3cm，BC=5cm，∠B=60°，G是CD的中点，E是边AD上的动点，EG的延长线与BC的延长线交于点F，连结CE，DF．

(1)、求证：四边形CEDF是平行四边形；

(2)、①当AE=cm时，四边形CEDF是矩形；
②当AE=cm时，四边形CEDF是菱形．
（直接写出答案，不需要说明理由）

查看试题解析