2016-2017学年福建省漳州市龙海市石码片八年级下学期期中数学试卷

试卷更新日期：2017-05-31 类型：期中考试

进入出卷网下载

一、选择题

1. 函数 $y = \frac{1}{x + 1}$ 中自变量x的取值范围是（）

A、x≠﹣1 B、x＞﹣1 C、x=﹣1 D、x＜﹣1

查看试题解析
2. 有理式 $\frac{2}{x}$ ， $\frac{1}{3}$ （x+y）， $\frac{x}{π - 3}$ ， $\frac{5}{a - x}$ ， $\frac{2 x - y}{4}$ 中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在平面直角坐标系中，点（3，﹣2）所在象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列式子成立的是（）

A、 $\frac{b}{a} + \frac{2}{b} = \frac{b + 2}{a + b}$ B、 $\frac{m + 3}{m} = 3$ C、 ${(\frac{y}{x^{2}})}^{2} = \frac{y^{2}}{x^{2}}$ D、 $\frac{n^{2}}{m n} = \frac{n}{m}$

查看试题解析
5. 有一种细菌的直径为0.000 000 012米，将这个数用科学记数法表示为（）

A、12×10⁸ B、12×10^﹣⁸ C、1.2×10^﹣⁸ D、1.2×10^﹣⁹

查看试题解析
6. 下列命题是假命题的是（）

A、平行四边形的对角线互相平分 B、平行四边形的对角相等 C、平行四边形是轴对称图形 D、平行四边形是中心对称图形

查看试题解析
7. 对于函数y= $\frac{k}{x}$ （k＞0），下列说法正确的是（）

A、y随x的增大而减小 B、y随x的增大而增大 C、当x＜0时，y随x的增大而减小 D、图象在第二、四象限内

查看试题解析
8. 若点M（x，y）的坐标满足x²﹣y²=0，则点M的位置是（）

A、在第二、四象限坐标轴夹角的平分线 B、在坐标轴夹角的平分线上 C、在第一、三象限坐标轴夹角的平分线上 D、在坐标轴上

查看试题解析
9. 在给定的条件中，能画出平行四边形的是（）

A、以60cm为一条对角线，20cm，34cm为两条邻边 B、以6cm，10cm为两条对角线，8cm为一边 C、以20cm，36cm为两条对角线，22cm为一边 D、以6cm为一条对角线，3cm，10cm为两条邻边

查看试题解析
10. 如图，点P是x轴正半轴上的一个动点，过点P作PQ⊥x轴交双曲线y= $\frac{1}{x}$ （x＞0）于点Q，连结OQ，当点P沿x轴的正方向运动时，Rt△QOP的面积（）

A、保持不变 B、逐渐减少 C、逐渐增大 D、无法确定

查看试题解析

二、填空题

11. $\frac{a^{2}}{a + 3} - \frac{9}{a + 3}$ = ．

查看试题解析
12. 当x=时，分式 $\frac{x - 3}{x + 2}$ 的值为0．

查看试题解析
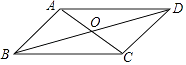
13. 在平行四边形ABCD中，若∠A：∠B=2：3，则∠C= ．

查看试题解析
14. 如图，已知▱ABCD周长为32cm，AC、BD交于点O，△BOC的周长比△AOB的周长多4cm，则AB的长是cm．

查看试题解析
15. 已知一次函数y=kx+b的自变量的取值范围是﹣3≤x≤6，相应函数的取值范围是﹣5≤y≤2，则一次函数的表达式为．

查看试题解析
16. 某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同．设原计划平均每天生产x台机器，根据题意列方程为．

查看试题解析

三、解答题

17. 计算：（ $\frac{1}{3}$ ﹣ $\frac{1}{5}$ ）×（ $\frac{1}{5}$ ）^﹣²÷|﹣ $\frac{1}{3}$ |+（﹣ $\frac{1}{5}$ ）⁰+（﹣0.25）²⁰⁰⁷×4²⁰⁰⁷ ．

查看试题解析
18. 先化简，再求值： $(\frac{1}{x - y} + \frac{1}{x + y}) \div \frac{x y}{x^{2} - y^{2}}$ ，其中x=2014，y=﹣2．

查看试题解析
19. 解分式方程： $\frac{1}{x - 1} = \frac{2}{x^{2} - 1}$

查看试题解析
20. 如图，在▱ABCD中，已知AD=5cm，AB=3cm，AE平分∠BAD交BC边于点E，求EC的长．

查看试题解析
21. 若关于x的方程 $\frac{2}{x - 1}$ + $\frac{5}{1 - x}$ = $\frac{m}{x^{2} - 1}$ 有增根，求增根和m的值．

查看试题解析
22. 已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同，甲、乙两人每天共加工35个零件，设甲每天加工x个A型零件．

(1)、求甲、乙每天各加工零件多少个？

(2)、根据市场预测，加工A型零件所获得的利润为m元/件（3≤m≤5），加工B型零件所获得的利润每件比A型少1元．求甲、乙每天加工的零件所获得的总利润P（元）与m的函数关系式，并求P的最大值和最小值．

查看试题解析
23. 我市某医药公司把一批药品运往外地，现有两种运输方式可供选择，方式一：使用快递公司的邮车运输，装卸收费400元，另外每公里再加收4元；方式二：使用快递公司的火车运输，装卸收费820元，另外每公里再加收2元，

(1)、请分别写出邮车、火车运输的总费用y₁、y₂（元）与运输路程x公里之间的函数关系式；

(2)、你认为选用哪种运输方式较好，为什么？

查看试题解析
24.
在平面直角坐标系中，已知直线AB 与y轴交于点A，与x轴交于点B，与双曲线y= $\frac{m}{x}$ （x＞0）交于点C（1，6）和点D（3，n）．作CE⊥y轴于E，DF⊥x轴于F．

(1)、求出m、n的值；

(2)、求出直线AB的解析式；

(3)、是否有△AEC≌△DFB，并说明理由．

查看试题解析
25. 已知直线AB：y=﹣ $\frac{1}{2}$ x+5与x轴、y轴分别交于点A、B，y轴上点C的坐标为（0，10）．

(1)、求A、B两点的坐标；

(2)、动点M从A点出发，以每秒1个单位长度的速度，沿x轴向左运动，连接CM．设点M的运动时间为t，△COM的面积为S，求S与t的函数关系式；（并标出自变量的取值范围）

(3)、直线AB与直线CM相交于点N，点P为y轴上一点，且始终保持PM+PN最短，当t为何值时，△COM≌△AOB，并求出此时点P的坐标．

查看试题解析