2016-2017学年安徽省合肥市瑶海区八年级下学期期中数学试卷

试卷更新日期：2017-05-31 类型：期中考试

进入出卷网下载

一、选择题

1. 在二次根式 $\sqrt{16 x^{3}}$ ，﹣ $\frac{\sqrt{2}}{3}$ ， $\sqrt{0.5}$ ， $\sqrt{\frac{a}{x}}$ ， $\sqrt{a^{2} - b^{2}}$ 中，最简二次根式有（）个．

A、1 B、2 C、3 D、4

查看试题解析
2. 若二次根式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是（）

A、x≤﹣1 B、x≥﹣1 C、x≤1 D、x≥1

查看试题解析
3. 若一元二次方程x²+2x+m=0有实数解，则m的取值范围是（）

A、m≤﹣1 B、m≤1 C、m≤4 D、 $m \leq \frac{1}{2}$

查看试题解析
4. 已知x=1是方程x²+ax+2=0的一个根，则方程的另一个根为（）

A、﹣2 B、2 C、﹣3 D、3

查看试题解析
5. 若a为方程x²+x﹣5=0的解，则a²+a+1的值为（）

A、12 B、6 C、9 D、16

查看试题解析
6. 为了美化环境，加大对绿化的投资.2008年用于绿化投资20万元，2010年用于绿化投资25万元，求这两年绿化投资的年平均增长率．设这两年绿化投资的年平均增长率为x，根据题意所列方程为（）

A、20x²=25 B、20（1+x）=25 C、20（1+x）+20（1+x）²=25 D、20（1+x）²=25

查看试题解析
7. 将方程x²+8x+9=0左边变成完全平方式后，方程是（　　）

A、（x+4）²=7 B、（x+4）²=25 C、（x+4）²=﹣9 D、（x+4）²=﹣7

查看试题解析
8. 下列命题中，是假命题的是（）

A、在△ABC中，若∠B=∠C﹣∠A，则△ABC是直角三角形 B、在△ABC中，若a²=（b+c）（b﹣c），则△ABC是直角三角形 C、在△ABC中，若∠A：∠B：∠C=3：4：5，则△ABC是直角三角形 D、在△ABC中，若a：b：c=3：4：5，则△ABC是直角三角形

查看试题解析
9. 一直角三角形的三边分别为2、3、x，那么以x为边长的正方形的面积为（）

A、13 B、5 C、13或5 D、4

查看试题解析
10. 如图，设正方体ABCD﹣A₁B₁C₁D₁的棱长为1，黑、白两个甲壳虫同时从点A出发，以相同的速度分别沿棱向前爬行，黑甲壳虫爬行的路线是AA₁→A₁D₁→…，白甲壳虫爬行的路线是AB→BB₁→…，并且都遵循如下规则：所爬行的第n+2与第n条棱所在的直线必须是既不平行也不相交（其中n是正整数）．那么当黑、白两个甲壳虫各爬行完第2013条棱分别停止在所到的正方体顶点处时，它们之间的距离是（）

A、0 B、1 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析

二、填空题

11. 若 $\sqrt{4 x^{2}}$ =2x，则x的取值范围是．

查看试题解析
12. 一元二次方程x（x﹣1）=x的解是．

查看试题解析
13. 若方程x²﹣ $\sqrt{m}$ x+n=0有两个相等实数根，则 $\frac{m}{n}$ 的值是．

查看试题解析
14. 如图所示，是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案，已知大正方形面积为49，小正方形面积为4，若用x，y表示直角三角形的两直角边（x＞y），下列四个说法：①x²+y²=49，②x﹣y=2，③2xy+4=49，④x+y=9．其中说法正确的结论有．

查看试题解析

三、解答题

15. 计算： ${(\sqrt{5} - 3)}^{2} + (\sqrt{11} + 3) (\sqrt{11} - 3)$

查看试题解析
16. （x﹣3）²+2x（x﹣3）=0．

查看试题解析
17. 如图，已知在△ABC中，CD⊥AB于D，AC=20，BC=15，DB=9．

(1)、求DC的长．

(2)、求AB的长．

查看试题解析
18. 在等腰△ABC中，三边分别为a、b、c，其中a=5，若关于x的方程x²+（b+2）x+6﹣b=0有两个相等的实数根，求△ABC的周长．

查看试题解析
19. 如图，在笔直的铁路上A、B两点相距25km，C、D为两村庄，DA=10km，CB=15km，DA⊥AB于A，CB⊥AB于B，现要在AB上建一个中转站E，使得C、D两村到E站的距离相等．求E应建在距A多远处？

查看试题解析
20. 如图所示，某工人师傅要在一个面积为15m²的矩形钢板上裁剪下两个相邻的正方形钢板当工作台的桌面，且要使大正方形的边长比小正方形的边长大1m．求裁剪后剩下的阴影部分的面积．

查看试题解析
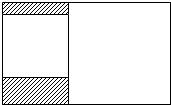21. 观察下列运算
①由（ $\sqrt{2} + 1$ ）（ $\sqrt{2} - 1$ ）=1，得 $\frac{1}{\sqrt{2} + 1}$ = $\sqrt{2} - 1$ ；
②由（ $\sqrt{3} + \sqrt{2}$ ）（ $\sqrt{3} - \sqrt{2}$ ）=1，得 $\frac{1}{\sqrt{3} + \sqrt{2}}$ = $\sqrt{3} - \sqrt{2}$ ；
③由（ $\sqrt{4}$ $+ \sqrt{3}$ ）（ $\sqrt{4}$ $- \sqrt{3}$ ）=1，得 $\frac{1}{\sqrt{4} + \sqrt{3}}$ = $\sqrt{4}$ $- \sqrt{3}$ ；
④由（ $\sqrt{5}$ $+ \sqrt{4}$ ）（ $\sqrt{5}$ $- \sqrt{4}$ ）=1，得 $\frac{1}{\sqrt{5} + \sqrt{4}}$ = $\sqrt{5}$ $- \sqrt{4}$ ；
…

(1)、通过观察，将你发现的规律用含有n的式子表示出来．

(2)、利用你发现的规律，计算： $\frac{1}{\sqrt{2} + 1}$ $+ \frac{1}{\sqrt{3} + \sqrt{2}}$ $+ \frac{1}{\sqrt{4} + \sqrt{3}}$ $+ \frac{1}{\sqrt{5} + \sqrt{4}}$ +…+ $\frac{1}{\sqrt{2017} + \sqrt{2016}}$ ．

查看试题解析
22. 某汽车销售公司2月份销售某厂汽车，在一定范围内，每辆汽车的进价与销售量有如下关系：
若当月仅售出1辆汽车，则该辆汽车的进价为30万元；每多售出1辆，所有售出的汽车的进价均降低0.1万元．月底厂家一次性返利给销售公司，每辆返利0.5万元．

(1)、若该公司当月售出7辆汽车，则每辆汽车的进价为多少万元？

(2)、如果汽车的售价为每辆31万元，该公司计划当月盈利12万元，那么需要售出多少辆汽车？（盈利=销售利润+返利）

查看试题解析
23. 定义：三边长和面积都是整数的三角形称为“整数三角形”．
数学学习小组的同学从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾依次相接组成三角形，进行探究活动．
小亮用12根火柴棒，摆成如图所示的“整数三角形”；
小颖分别用24根和30根火柴棒摆出直角“整数三角形”；
小辉受到小亮、小颖的启发，分别摆出三个不同的等腰“整数三角形”．

(1)、请你画出小颖和小辉摆出的“整数三角形”的示意图；

(2)、你能否也从中取出若干根，按下列要求摆出“整数三角形”，如果能，请画出示意图；如果不能，请说明理由．
①摆出等边“整数三角形”；
②摆出一个非特殊（既非直角三角形，也非等腰三角形）“整数三角形”．

查看试题解析