2016-2017学年安徽省滁州市明光市八年级下学期期中数学试卷
试卷更新日期:2017-05-31 类型:期中考试
一、选择题
-
1. 下列根式与﹣ 是同类二次根式的是( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、8 ﹣2 =6 B、5 +5 =10 C、4 ÷2 =2 D、4 ×2 =83. 一元二次方程x2+2x+1=0的根的情况( )A、有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根4. 五根小木棒,其长度分别为7,15,20,24,25,现将它们摆成两个直角三角形,如图,其中正确的是( )A、
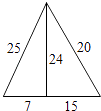 B、
B、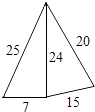 C、
C、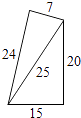 D、
D、 5.
5.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2 , 求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( )
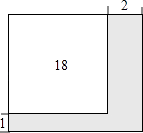 A、(x+1)(x+2)=18 B、x2﹣3x+16=0 C、(x﹣1)(x﹣2)=18 D、x2+3x+16=06. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( )
A、(x+1)(x+2)=18 B、x2﹣3x+16=0 C、(x﹣1)(x﹣2)=18 D、x2+3x+16=06. 如图,直线l上有三个正方形a,b,c,若a,c的面积分别为3和4,则b的面积为( ) A、3 B、4 C、5 D、77. 给出一种运算:对于函数y=xn , 规定y′=nxn﹣1 . 例如:若函数y=x4 , 则有y′=4x3 . 已知函数y=x3 , 则方程y′=12的解是( )A、x1=4,x2=﹣4 B、x1=2,x2=﹣2 C、x1=x2=0 D、x1=2 ,x2=﹣28. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣4x+3=0的根,则该三角形的周长可以是( )A、5 B、7 C、5或7 D、109. 已知一元二次方程x2﹣4x﹣3=0两根为m,n,则m2﹣mn+n2的值为( )A、25 B、16 C、9 D、710. 如图,若将如图(1)所示的正方形剪成四块,恰能拼成如图(2)所示的长方形,设a=1,则b的值为( )
A、3 B、4 C、5 D、77. 给出一种运算:对于函数y=xn , 规定y′=nxn﹣1 . 例如:若函数y=x4 , 则有y′=4x3 . 已知函数y=x3 , 则方程y′=12的解是( )A、x1=4,x2=﹣4 B、x1=2,x2=﹣2 C、x1=x2=0 D、x1=2 ,x2=﹣28. 已知等腰三角形的腰和底的长分别是一元二次方程x2﹣4x+3=0的根,则该三角形的周长可以是( )A、5 B、7 C、5或7 D、109. 已知一元二次方程x2﹣4x﹣3=0两根为m,n,则m2﹣mn+n2的值为( )A、25 B、16 C、9 D、710. 如图,若将如图(1)所示的正方形剪成四块,恰能拼成如图(2)所示的长方形,设a=1,则b的值为( ) A、 B、 C、 D、 +1
A、 B、 C、 D、 +1二、填空题
-
11. 使式子 有意义的实数x的取值范围 .12. 设x1、x2是方程x2﹣4x+m=0的两个根,且x1+x2﹣x1x2=1.则m= .13. 如图,在△ABC中,AB=AC=5,BC=6,点M为BC中点,MN⊥AC于点N,则MN的长是 .
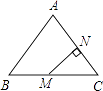 14. 如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是 . (把所有正确答案的序号都填在横线上)
14. 如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是 . (把所有正确答案的序号都填在横线上)
三、解答题
-
15. 计算: .16. 解方程:2x2﹣3x﹣1=0.17. 如图,在边长为1的小正方形组成的网格中,四边形ABCD的四个顶点都在格点上,请按要求完成下列各题.
 (1)、线段AB的长为 , BC的长为 , CD的长为;(2)、连接AC,通过计算说明△ACD和△ABC是什么特殊三角形.18. 关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.(1)、求m的取值范围;(2)、当m取满足条件的最小整数时,求方程的解.19. 如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长.
(1)、线段AB的长为 , BC的长为 , CD的长为;(2)、连接AC,通过计算说明△ACD和△ABC是什么特殊三角形.18. 关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根.(1)、求m的取值范围;(2)、当m取满足条件的最小整数时,求方程的解.19. 如图,折叠矩形的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EC的长. 20. 若一元二次方程ax2=b(ab>0)的两根分别为m+1与2m﹣4.(1)、求m的值;(2)、求 的值.21. 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
20. 若一元二次方程ax2=b(ab>0)的两根分别为m+1与2m﹣4.(1)、求m的值;(2)、求 的值.21. 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
 (1)、作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=;(2)、请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;(3)、利用勾股定理求出AD的长,再计算三角形的面积.22. 现有一组有规律的数:1,﹣1, ,﹣ , ,﹣ ,1,﹣1, ,﹣ , ,﹣ …其中1,﹣1, ,﹣ , ,﹣ 这六个数按此规律重复出现.(1)、第50个数是什么数?(2)、把从第1个数开始的前2017个数相加,结果是多少?(3)、从第1个数起,把连续若干个数的平方相加起来,如果和为520,那么一共是多少和数的平方相加?23. 某商业街有店面房共195间,2014年平均每间店面房的年租金为10万元,由于物价上涨,到2016年平均每间店面房的年租金上涨到了12.1万元,据预测,当每间的年租金定为12.1万元时,可全部租出;若每间的年租金每增加1万元,就要少租出10间.该商业街管委会要为租出的商铺每间每年交各种费用1.1万元,未租出的商铺每间每年交各种费用5000元.(1)、求2014年至2016年平均每间店面房年租金的平均增长率;(2)、当每间店面房的年租金上涨多少万元时,该商业街的年收益(收益=租金﹣各种费用)为2305万元?
(1)、作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=;(2)、请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;(3)、利用勾股定理求出AD的长,再计算三角形的面积.22. 现有一组有规律的数:1,﹣1, ,﹣ , ,﹣ ,1,﹣1, ,﹣ , ,﹣ …其中1,﹣1, ,﹣ , ,﹣ 这六个数按此规律重复出现.(1)、第50个数是什么数?(2)、把从第1个数开始的前2017个数相加,结果是多少?(3)、从第1个数起,把连续若干个数的平方相加起来,如果和为520,那么一共是多少和数的平方相加?23. 某商业街有店面房共195间,2014年平均每间店面房的年租金为10万元,由于物价上涨,到2016年平均每间店面房的年租金上涨到了12.1万元,据预测,当每间的年租金定为12.1万元时,可全部租出;若每间的年租金每增加1万元,就要少租出10间.该商业街管委会要为租出的商铺每间每年交各种费用1.1万元,未租出的商铺每间每年交各种费用5000元.(1)、求2014年至2016年平均每间店面房年租金的平均增长率;(2)、当每间店面房的年租金上涨多少万元时,该商业街的年收益(收益=租金﹣各种费用)为2305万元?