2016年广东省深圳市中考数学三模试卷
试卷更新日期:2017-05-31 类型:中考模拟
一、选择题
-
1. 的倒数是( )A、﹣2 B、 C、2 D、2. 据相关报道,截止到今年四月,我国已完成5.78万个农村教学点的建设任务.5.78万可用科学记数法表示为( )A、5.78×103 B、57.8×103 C、0.578×104 D、5.78×1043.
在下列四种图形变换中,本题图案不包含的变换是( )
 A、位似 B、旋转 C、轴对称 D、平移4. 下列运算正确的是( )A、a2+a3=a5 B、(﹣2a2)3=﹣6a6 C、(2a+1)(2a﹣1)=2a2﹣1 D、(2a3﹣a2)÷a2=2a﹣15. 小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.则向上的一面的点数大于4的概率为( )A、 B、 C、 D、6. 甲、乙、丙、丁四名射击运动员参加了预选赛,他们射击成绩的平均环数 及方差s2如表所示.
A、位似 B、旋转 C、轴对称 D、平移4. 下列运算正确的是( )A、a2+a3=a5 B、(﹣2a2)3=﹣6a6 C、(2a+1)(2a﹣1)=2a2﹣1 D、(2a3﹣a2)÷a2=2a﹣15. 小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.则向上的一面的点数大于4的概率为( )A、 B、 C、 D、6. 甲、乙、丙、丁四名射击运动员参加了预选赛,他们射击成绩的平均环数 及方差s2如表所示.甲
乙
丙
丁
8
9
9
8
s2
1
1
1.2
1.3
如果选出一个成绩较好且状态稳定的运动员去参赛,那么应选( )
A、甲 B、乙 C、丙 D、丁7. 若 ,则xy的值为( )A、5 B、6 C、﹣6 D、﹣88. 如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.设AP=x,△PBE的面积为y.则能够正确反映y与x之间的函数关系的图象是( )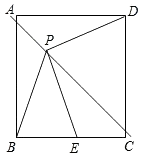 A、
A、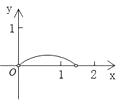 B、
B、 C、
C、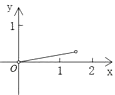 D、
D、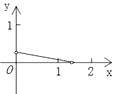 9. 已知下列命题:
9. 已知下列命题:①同位角相等;
②若a>b>0,则 ;
③对角线相等且互相垂直的四边形是正方形;
④抛物线y=x2﹣2x与坐标轴有3个不同交点;
⑤边长相等的多边形内角都相等.
其中正确的命题有( )
A、1个 B、2个 C、3个 D、4个10. 如图,A、B、C、D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( ) A、40° B、45° C、50° D、55°11. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“
A、40° B、45° C、50° D、55°11. 如图1,将一个边长为a的正方形纸片剪去两个小矩形,得到一个“ ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( ) A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b12. 已知反比例函数y= 的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为( )
A、2a﹣3b B、4a﹣8b C、2a﹣4b D、4a﹣10b12. 已知反比例函数y= 的图象如图,则二次函数y=2kx2﹣4x+k2的图象大致为( )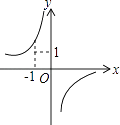 A、
A、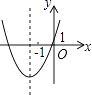 B、
B、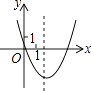 C、
C、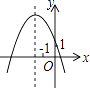 D、
D、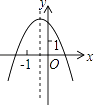
二、填空题
-
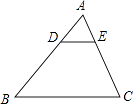
13. 因式分解:xy2﹣4xy+4x= .14. 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:DB=1:2,AE=2,则AC= .
 15. 如图,反比例函数y= 的图象与经过原点的直线相交于点A、B,已知A的坐标为(﹣2,1),则点B的坐标为 .
15. 如图,反比例函数y= 的图象与经过原点的直线相交于点A、B,已知A的坐标为(﹣2,1),则点B的坐标为 . 16. 如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为 .
16. 如图,以边长为1的正方形的四边中点为顶点作四边形,再以所得四边形四边中点为顶点作四边形,…依次作下去,图中所作的第n个四边形的周长为 .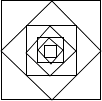
三、解答题
-
17. 计算: .18. 化简求值: + ÷a,其中a=﹣2.19. 2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).
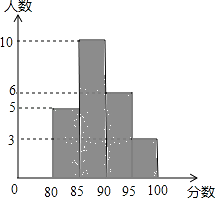 (1)、分数段在范围的人数最多;(2)、全校共有多少人参加比赛?(3)、学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.20. 如图,正方形ABCD的边长为1cm,AC是对角线,AE平分∠BAC,EF⊥AC于F.
(1)、分数段在范围的人数最多;(2)、全校共有多少人参加比赛?(3)、学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.20. 如图,正方形ABCD的边长为1cm,AC是对角线,AE平分∠BAC,EF⊥AC于F.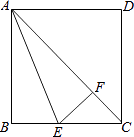 (1)、求证:BE=EF.(2)、求tan∠EAF的值.21. 市园林处为了对一段公路进行绿化,计划购买A,B两种风景树共900棵.A,B两种树的相关信息如下表:
(1)、求证:BE=EF.(2)、求tan∠EAF的值.21. 市园林处为了对一段公路进行绿化,计划购买A,B两种风景树共900棵.A,B两种树的相关信息如下表:品种 项目
单价(元/棵)
成活率
A
80
92%
B
100
98%
若购买A种树x棵,购树所需的总费用为y元.
(1)、求y与x之间的函数关系式;(2)、若购树的总费用不超过82 000元,则购A种树不少于多少棵?(3)、若希望这批树的成活率不低于94%,且使购树的总费用最低,应选购A,B两种树各多少棵?此时最低费用为多少?22. 如图所示,抛物线m:y=ax2+b(a<0,b>0)与x轴于点A、B(点A在点B的左侧),与y轴交于点C.将抛物线m绕点B旋转180°,得到新的抛物线n,它的顶点为C1 , 与x轴的另一个交点为A1 .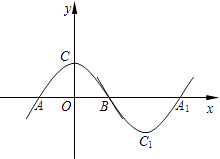 (1)、当a=﹣1,b=1时,求抛物线n的解析式;(2)、四边形AC1A1C是什么特殊四边形,请写出结果并说明理由;(3)、若四边形AC1A1C为矩形,请求出a,b应满足的关系式.23. 如图①,在平面直角坐标系中,直线y=﹣ x+ 与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.
(1)、当a=﹣1,b=1时,求抛物线n的解析式;(2)、四边形AC1A1C是什么特殊四边形,请写出结果并说明理由;(3)、若四边形AC1A1C为矩形,请求出a,b应满足的关系式.23. 如图①,在平面直角坐标系中,直线y=﹣ x+ 与x轴交于C点,与y轴交于点E,点A在x轴的负半轴,以A点为圆心,AO为半径的圆与直线的CE相切于点F,交x轴负半轴于另一点B.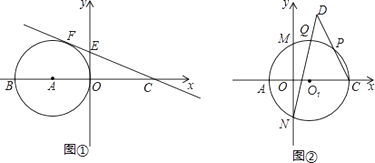 (1)、求⊙A的半径;(2)、连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.(3)、如图②,以AC为直径作⊙O1交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.
(1)、求⊙A的半径;(2)、连BF、AE,则BF与AE之间有什么位置关系?写出结论并证明.(3)、如图②,以AC为直径作⊙O1交y轴于M,N两点,点P是弧MC上任意一点,点Q是弧PM的中点,连CP,NQ,延长CP,NQ交于D点,求CD的长.