2016年广东省深圳市盐田区中考数学二模试卷
试卷更新日期:2017-05-31 类型:中考模拟
一、选择题
-
1. 下列说法正确的是( )A、﹣1的相反数是1 B、﹣1的倒数是1 C、﹣1的平方根是1 D、﹣1的立方根是12. 次数为3的单项式可以是( )A、3ab B、ab2 C、a3+b3 D、a3b3. 与4﹣最接近的整数是( )
A、0 B、1 C、2 D、34. 如图是边长为1的六个小正方形组成的平面图形,经过折叠能围成一个正方体,那么点A、B在围成的正方体上相距( ) A、0 B、1 C、 D、5. 当|k﹣2b|+ =0时,直线y=kx+b经过点( )A、(﹣1,﹣1) B、(﹣1,1) C、(﹣1,﹣3) D、(﹣1,3)6. 在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是( )A、正比例函数 B、反比例函数 C、图象不经过原点的一次函数 D、二次函数7. 抛物线y=﹣x2+6x﹣9的顶点为A,与y轴的交点为B,如果在抛物线上取点C,在x轴上取点D,使得四边形ABCD为平行四边形,那么点D的坐标是( )A、(﹣6,0) B、(6,0) C、(﹣9,0) D、(9,0)8. 函数y=ax2+bx+a+b(a≠0)的图象可能是( )A、
A、0 B、1 C、 D、5. 当|k﹣2b|+ =0时,直线y=kx+b经过点( )A、(﹣1,﹣1) B、(﹣1,1) C、(﹣1,﹣3) D、(﹣1,3)6. 在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是( )A、正比例函数 B、反比例函数 C、图象不经过原点的一次函数 D、二次函数7. 抛物线y=﹣x2+6x﹣9的顶点为A,与y轴的交点为B,如果在抛物线上取点C,在x轴上取点D,使得四边形ABCD为平行四边形,那么点D的坐标是( )A、(﹣6,0) B、(6,0) C、(﹣9,0) D、(9,0)8. 函数y=ax2+bx+a+b(a≠0)的图象可能是( )A、 B、
B、 C、
C、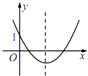 D、
D、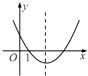 9. 关于x的方程 有增根,那么a=( )A、﹣2 B、0 C、1 D、310. 抛物线y=x2+bx的对称轴经过点(2,0),那么关于x的方程x2+bx=5的两个根是( )A、0,4 B、1,5 C、﹣1,5 D、1,﹣511. 如图,经过点A1(1,0)作x轴的垂线与直线l:y= x相交于点B1 , 以O为圆心,OB1为半径画弧与x轴相交于点A2;经过点A2作x轴的垂线与直线l相交于点B2 , 以O为圆心、OB2为半径画弧与x轴相交于点A3;…依此类推,点A5的坐标是( )
9. 关于x的方程 有增根,那么a=( )A、﹣2 B、0 C、1 D、310. 抛物线y=x2+bx的对称轴经过点(2,0),那么关于x的方程x2+bx=5的两个根是( )A、0,4 B、1,5 C、﹣1,5 D、1,﹣511. 如图,经过点A1(1,0)作x轴的垂线与直线l:y= x相交于点B1 , 以O为圆心,OB1为半径画弧与x轴相交于点A2;经过点A2作x轴的垂线与直线l相交于点B2 , 以O为圆心、OB2为半径画弧与x轴相交于点A3;…依此类推,点A5的坐标是( ) A、(8,0) B、(12,0) C、(16,0) D、(32,0)
A、(8,0) B、(12,0) C、(16,0) D、(32,0)二、填空题
-
12. 月初,明斯克航母告别盐田,据不完全估算,16年间累计接待游客11000000人次,11000000用科学记数法表示是 .13. 如图,在△ABC中,∠ABC=90°,∠C=50°,以A为圆心、AB为半径的弧与AC相交于点D,那么∠CBD=°.
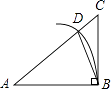 14. 当x=a或x=b(a≠b)时,整式x2+x的值相等,那么当x=a+b时,分式 的值是 .15. 如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD= .
14. 当x=a或x=b(a≠b)时,整式x2+x的值相等,那么当x=a+b时,分式 的值是 .15. 如图,将△ABC沿角平分线BD所在直线翻折,顶点A恰好落在边BC的中点E处,AE=BD,那么tan∠ABD= .
三、解答题
-
16. 根据题意解答(1)、计算: +|2﹣ |;(2)、当关于x的方程x2﹣2x+c=0有实数根时,求c的取值范围.17. 小凡把果树林分为两部分,左地块用新技术管理,右地块用老方法管理,管理成本相同,她在左、右两地块上各随机选取20棵果树,按产品分成甲、乙、丙、丁四个等级(数据分组包括左端点不包括右端点),并制作如下两幅不完整的统计图:
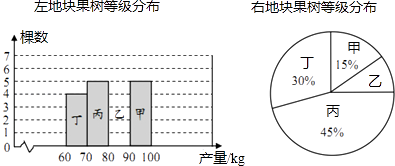 (1)、补齐左地块统计图,求右地块乙级所对应的圆心角的度数;(2)、比较两地块的产量水平,并说明试验结果;(3)、在左地块随机抽查一棵果树,求该果树产量为乙级的概率.18. 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m.
(1)、补齐左地块统计图,求右地块乙级所对应的圆心角的度数;(2)、比较两地块的产量水平,并说明试验结果;(3)、在左地块随机抽查一棵果树,求该果树产量为乙级的概率.18. 如图,某高楼顶部有一信号发射塔,小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β,AD=18m,CD=78m. (1)、用α和β的三角函数表示CE;(2)、当α=30°、β=60°时,求EF(结果精确到1m).
(1)、用α和β的三角函数表示CE;(2)、当α=30°、β=60°时,求EF(结果精确到1m).(参考数据: ≈1.414, ≈1.732)
19. 一般情况下,学生注意力上课后逐渐增强,中间有段时间处于较理想的稳定状态,随后开始分散.实验结果表明,学生注意力指数y随时间x(min)的变化规律如图所示(其中AB、BC分别为线段,CD为双曲线的一部分): (1)、上课后第5min与第30min相比较,何时学生注意力更集中?(2)、某道难题需连续讲19min,为保证效果,学生注意力指数不宜低于36,老师能否在所需要求下讲完这道题?20. 如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.
(1)、上课后第5min与第30min相比较,何时学生注意力更集中?(2)、某道难题需连续讲19min,为保证效果,学生注意力指数不宜低于36,老师能否在所需要求下讲完这道题?20. 如图,四边形ABCD是⊙O的内接四边形,AD的延长线与BC的延长线相交于点E,DC=DE.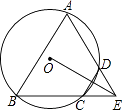 (1)、求证:∠A=∠AEB;(2)、如果DC⊥OE,求证:△ABE是等边三角形.21. 抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.(1)、用含a的式子表示点B的坐标;(2)、经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.22. 如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
(1)、求证:∠A=∠AEB;(2)、如果DC⊥OE,求证:△ABE是等边三角形.21. 抛物线y=ax2﹣2x与x轴正半轴相交于点A,顶点为B.(1)、用含a的式子表示点B的坐标;(2)、经过点C(0,﹣2)的直线AC与OB(O为原点)相交于点D,与抛物线的对称轴相交于点E,△OCD≌△BED,求a的值.22. 如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t. (1)、当t=1时,求点E的坐标;(2)、设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);(3)、当OE取最小值时,求点E的坐标.
(1)、当t=1时,求点E的坐标;(2)、设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);(3)、当OE取最小值时,求点E的坐标.