2016年广东省深圳市十七校联考中考数学模拟试卷
试卷更新日期：2017-05-31 类型：中考模拟
一、选择题
-
1. 的倒数是（ ）A、﹣2 B、2 C、 D、2. 2015年初，一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃，将300000用科学记数法表示为（ ）A、3×106 B、3×105 C、0.3×106 D、30×1043. 下列计算正确的是（ ）A、a3•a4=a12 B、（a3）4=a7 C、（a2b）3=a6b3 D、a3÷a4=a（a≠0）4. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
5. 一个几何体的三视图如图所示，这个几何体是（ ）
A、棱柱 B、圆柱 C、圆锥 D、球6. 为了解某班学生每天使用零花钱的情况，小红随机调查了15名同学，结果如下表：每天使用零花钱
（单位：元）
1
2
3
5
6
人 数
2
5
4
3
1
则这15名同学每天使用零花钱的众数和中位数分别是（ ）
A、3，3 B、2，3 C、2，2 D、3，57. 阳光公司销售一种进价为21元的电子产品，按标价的九折销售，仍可获利20%，则这种电子产品的标价为（ ）A、26元 B、27元 C、28元 D、29元8. 下列不等式变形正确的是（ ）A、由a＞b，得a﹣2＜b﹣2 B、由a＞b，得|a|＞|b| C、由a＞b，得﹣2a＜﹣2b D、由a＞b，得a2＞b29. 四个命题：①三角形的一条中线能将三角形分成面积相等的两部分；②有两边和其中一边的对角分别相等的两个三角形全等；③点P（1，2）关于原点的对称点坐标为（﹣1，﹣2）；④对角线互相垂直的四边形是菱形，其中正确的是（ ）A、①② B、①③ C、②③ D、③④10. 如图，直线AB与⊙O相切于点A，⊙O的半径为2，若∠OBA=30°，则AB的长为（ ）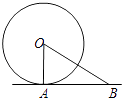
A、4 B、4 C、2 D、211. 如图是二次函数y=ax2+bx+c过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac，②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确结论是（ ）
A、②④ B、①④ C、②③ D、①③12. 如图，在直角梯形ABCD中，DC∥AB，∠DAB=90°，AC⊥BC，AC=BC，∠ABC的平分线分别交AD、AC于点E，F，则 的值是（ ）
A、 B、 C、 +1 D、二、填空题
-
13. 因式分解：x3y﹣xy= ．14. 小亮与小明一起玩“石头、剪刀、布”的游戏，两同学同时出“剪刀”的概率是 ．15.
“五一”国际劳动节，广场中央摆放着一个正六边形的鲜花图案，如图所示，已知第一层摆黄色花，第二层摆红色花，第三层是紫色花，第四层摆黄色花…由里向外依次按黄、红、紫的颜色摆放，那么第10层应摆盆花．
16. 如图，△AOB与△ACD均为正三角形，且顶点B、D均在双曲线y= （x＞0）上，点A、C在x轴上，连接BC交AD于点P，则△OBP的面积= ．
三、解答题
-
17. 计算：﹣22+ +（3﹣π）0﹣|﹣3|18. 先化简（ ）+（1﹣ ），然后从﹣ ＜x＜ 范围内选取一个合适的整数作为x的值代入求值．19. 垃圾的分类处理与回收利用，可以减少污染，节省资源．某城市环保部门为了提高宣传实效，抽样调查了部分居民小区一段时间内生活垃圾的分类情况，其相关信息如下：
根据图表解答下列问题：
(1)、请将条形统计图补充完整；(2)、在抽样数据中，产生的有害垃圾共吨；(3)、调查发现，在可回收物中塑料类垃圾占 ，每回收1吨塑料类垃圾可获得0.7吨二级原料．假设该城市每月产生的生活垃圾为5 000吨，且全部分类处理，那么每月回收的塑料类垃圾可以获得多少吨二级原料？20. 如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8．以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．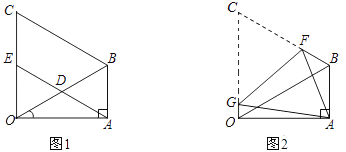
(1)、求证：四边形ABCE是平行四边形；(2)、如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．21. 山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．(1)、今年A型车每辆售价多少元？（列方程解答）(2)、该车行计划今年新进一批A型车和B型车共60辆，A型车的进货价为每辆1100元，销售价与（1）相同；B型车的进货价为每辆1400元，销售价为每辆2000元，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
