2016年广东省深圳市南山区五校联考中考数学三模试卷

试卷更新日期：2017-05-31 类型：中考模拟

进入出卷网下载

一、选择题

1. 2的倒数是（）

A、﹣2 B、2 C、 $\frac{1}{2}$ D、﹣ $\frac{1}{2}$

查看试题解析
2. 横跨深圳及香港之间的深圳湾大桥（ShenzhenBayBridge）是中国唯一倾斜的独塔单索面桥，大桥全长4 770米，这个数字用科学记数法表示为（保留两个有效数字）（）

A、47×10² B、4.7×10³ C、4.8×10³ D、5.0×10³

查看试题解析
3. 如图，是轴对称图形但不是中心对称图形的是（）

A、线段 B、三角形 C、正方形 D、圆

查看试题解析
4. 下列运算正确的是（　　）

A、2a²+3a³=5a⁵ B、a⁶÷a³=a² C、（﹣a³）²=a⁶ D、（x+y）²=x²+y²

查看试题解析
5. 如图是由八个相同小正方体组合而成的几何体，则其俯视图是（）

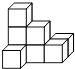A、 B、 C、 D、

查看试题解析
6. 在﹣2，1，2，1，4，6中正确的是（）

A、平均数3 B、众数是﹣2 C、中位数是1 D、极差为8

查看试题解析
7. 某商品的进价是80元，打8折售出后，仍可获利10%，你认为标在标签上的价格为（）

A、110元 B、120元 C、150元 D、160元

查看试题解析
8. 如图，沿AE折叠矩形纸片ABCD，使点D落在BC边的点F处已知AB=8，BC=10，则tan∠EFC的值为（）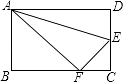

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
9.
在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处，观察到飞艇底部标志P处的仰角为45°，又观其在湖中之像的俯角为60°．则飞艇离开湖面的高度（　　）

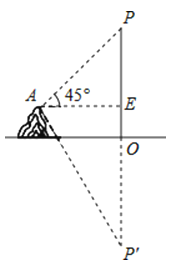A、25 $\sqrt{3}$ +75 B、50 $\sqrt{3}$ +50 C、75 $\sqrt{3}$ +75 D、50 $\sqrt{3}$ +100

查看试题解析
10.
如图，二次函数y=ax²+bx+c的图象与x轴的交点的横坐标分别为﹣1，3，则下列结论正确的个数有（　　）
①ac＜0；②2a+b=0；③4a+2b+c＞0；④对于任意x均有ax²+bx≥a+b．

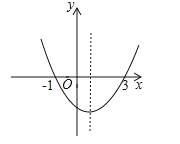A、1 B、2 C、3 D、4

查看试题解析
11. 已知：如图，∠MON=45°，OA₁=1，作正方形A₁B₁C₁A₂ ，面积记作S₁；再作第二个正方形A₂B₂C₂A₃ ，面积记作S₂；继续作第三个正方形A₃B₃C₃A₄ ，面积记作S₃；点A₁、A₂、A₃、A₄…在射线ON上，点B₁、B₂、B₃、B₄…在射线OM上，…依此类推，则第6个正方形的面积S₆是（）

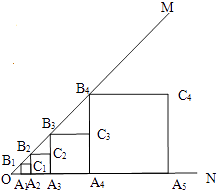A、256 B、900 C、1024 D、4096

查看试题解析

二、填空题

12. 分解因式：ax²﹣4ax+4a=

查看试题解析
13. 一个口袋有3个黑球和若干个白球，在不允许将球倒出来的前提下，小明为估计其中的白秋数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，再放回口袋中，…，不断重复上述过程，小明共摸了100次，其中20次摸到黑球．根据上述数据，小明正估计口袋中的白球的个数是．

查看试题解析
14. 如图，已知⊙O的直径AB与弦CD相交于点E，AB⊥CD，⊙O的切线BF与弦AD的延长线相交于点F．若⊙O的半径为5，cos∠BCD= $\frac{4}{5}$ ，那么线段AD= ．

查看试题解析
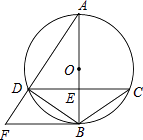15. 已知四边形OABC是菱形，CD⊥x轴，垂足为D，函数 $y = \frac{8}{x}$ 的图象经过点C，且与AB交于点E，若OD=2，则△OCE的面积为．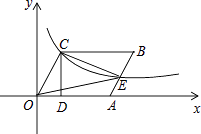

查看试题解析

三、解答题：

16. 计算：|﹣ $\sqrt{8}$ |+ ${(\frac{1}{3})}^{- 1}$ ﹣4sin45°﹣ ${(\sqrt{2016} - \sqrt{2015})}^{0}$ ．

查看试题解析
17. 先化简 $(\frac{a + 2}{a^{2} - 2 a} + \frac{8}{4 - a^{2}}) \div \frac{a - 2}{a}$ ，然后从﹣3＜a＜3的范围内选取一个你认为合适的整数作为a的值代入求值．

查看试题解析
18. 今年以来，我国持续大面积的雾霾天气让环保和健康问题成为焦点．为了调查学生对雾霾天气知识的了解程度，某校在学生中做了一次抽样调查，调查结果共分为四个等级：A．非常了解；B．比较了解；C．基本了解；D．不了解．根据调查统计结果，绘制了不完整的三种统计图表．
对雾霾了解程度的统计表：
对雾霾的了解程度
百分比
A．非常了解
5%
B．比较了解
m
C．基本了解
45%
D．不了解
n
请结合统计图表，回答下列问题．
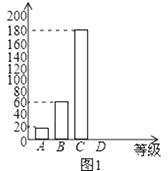
对雾霾天气了解程度的条形统计图
对雾霾天气了解程度的扇形统计图

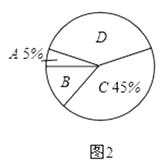(1)、本次参与调查的学生共有人，m= ， n=；

(2)、图2所示的扇形统计图中D部分扇形所对应的圆心角是度；

(3)、请补全图1示数的条形统计图；

(4)、根据调查结果，学校准备开展关于雾霾知识竞赛，某班要从“非常了解”态度的小明和小刚中选一人参加，现设计了如下游戏来确定，具体规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去．请用树状图或列表法说明这个游戏规则是否公平．

查看试题解析
19. 为了提高服务质量，某宾馆决定对甲、乙两种套房进行星级提升，已知甲种套房提升费用比乙种套房提升费用少3万元，如果提升相同数量的套房，甲种套房费用为625万元，乙种套房费用为700万元．

(1)、甲、乙两种套房每套提升费用各多少万元？

(2)、如果需要甲、乙两种套房共80套，市政府筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于甲、乙种套房星级提升，市政府对两种套房的提升有几种方案？哪一种方案的提升费用最少？

(3)、在（2）的条件下，根据市场调查，每套乙种套房的提升费用不会改变，每套甲种套房提升费用将会提高a万元（a＞0），市政府如何确定方案才能使费用最少？

查看试题解析
20. 如图，正方形ABGD中，AB=AD=6，梯形ABCD中，DE⊥DC交AB于E，DF平分∠EDC交BC于F，连结EF．

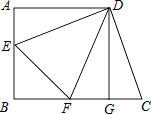(1)、证明：EF=CF；

(2)、当 $\frac{A E}{A D} = \frac{1}{3}$ 时，求EF的长．

查看试题解析
21.
如图，在平面直角坐标系中，圆D与y轴相切于点C（0，4），与x轴相交于A、B两点，且AB=6．

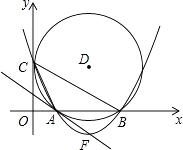(1)、则D点的坐标是（，），圆的半径为；

(2)、sin∠ACB=；经过C、A、B三点的抛物线的解析式；

(3)、设抛物线的顶点为F，证明直线FA与圆D相切；

(4)、在x轴下方的抛物线上，是否存在一点N，使△CBN面积最大，最大值是多少，并求出N点坐标．

查看试题解析
22.
如图，抛物线与x轴交于A（x₁ ， 0）、B（x₂ ， 0）两点，且x₁＜x₂ ，与y轴交于点C（0，﹣4），其中x₁ ， x₂是方程x²﹣4x﹣12=0的两个根．

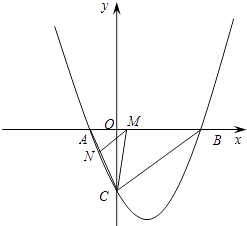(1)、求抛物线的解析式；

(2)、点M是线段AB上的一个动点，过点M作MN∥BC，交AC于点N，连接CM，当△CMN的面积最大时，求点M的坐标；

(3)、点D（4，k）在（1）中抛物线上，点E为抛物线上一动点，在x轴上是否存在点F，使以A、D、E、F为顶点的四边形是平行四边形？如果存在，求出所有满足条件的点F的坐标；若不存在，请说明理由．

查看试题解析

对雾霾的了解程度	百分比
A．非常了解	5%
B．比较了解	m
C．基本了解	45%
D．不了解	n