广东省深圳市北师大附中2016年中考数学二模试卷

试卷更新日期：2017-05-31 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2的相反数是（）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 太阳的半径约为696000km，把696000这个数用科学记数法表示为（）

A、6.96×10³ B、69.6×10⁵ C、6.96×10⁵ D、6.96×10⁶

查看试题解析
3. 不等式组 ${\begin{cases} x + 2 \geq 0 \\ x - 1 \leq 0 \end{cases}$ 的解集是（）

A、﹣2≤x≤1 B、﹣2＜x＜1 C、x≤﹣1 D、x≥2

查看试题解析
4. 下列计算正确的是（）

A、a³÷a²=a³•a^﹣² B、 $\sqrt{a^{2}} = a$ C、2a²+a²=3a⁴ D、（a﹣b）²=a²﹣b²

查看试题解析
5. 如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 一副三角板有两个直角三角形，如图叠放在一起，则∠α的度数是（）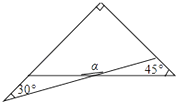

A、165° B、120° C、150° D、135°

查看试题解析
7. 在△ABC中，∠C=90°，BC=4cm，AC=3cm，把△ABC绕点A顺时针旋转90°后，得到△A₁B₁C₁（如图所示），则线段AB所扫过的面积为（）

A、5 $\sqrt{2}$ B、 $\frac{25}{4}$ πcm² C、 $\frac{25}{2}$ πcm² D、5πcm²

查看试题解析
8. 已知m，n是关于x的一元二次方程x²﹣3x+a=0的两个解，若（m﹣1）（n﹣1）=﹣6，则a的值为（）

A、﹣10 B、4 C、﹣4 D、10

查看试题解析
9. 2010年3月份，某市市区一周空气质量报告中某项污染指数的数据是：31，35，31，34，30，32，31，这组数据的中位数、众数分别是（　　）

A、32，31 B、31，32 C、31，31 D、32，35

查看试题解析
10. 在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2），以原点O为位似中心，相似比为 $\frac{1}{2}$ ，把△EFO缩小，则点E的对应点E′的坐标是（）

A、（﹣2，1） B、（﹣8，4） C、（﹣8，4）或（8，﹣4） D、（﹣2，1）或（2，﹣1）

查看试题解析
11. 如图，有一矩形纸片ABCD，AB=6，AD=8，将纸片折叠使AB落在AD边上，折痕为AE，再将△ABE以BE为折痕向右折叠，AE与CD交于点F，则 $\frac{C F}{C D}$ 的值是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
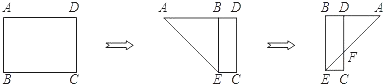12. 小轩从如图所示的二次函数y=ax²+bx+c（a≠0）的图象中，观察得出了下面五条信息：
①ab＞0；②a+b+c＜0；③b+2c＞0；④a﹣2b+4c＞0；⑤ $a = \frac{3}{2} b$ ．
你认为其中正确信息的个数有（）

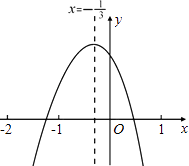A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 分解因式：ax²+2ax﹣3a= ．

查看试题解析
14. 用半径为10cm，圆心角为216°的扇形做成一个圆锥的侧面，则这个圆锥的高为cm．

查看试题解析
15.
如图，两建筑物的水平距离BC为18m，从A点测得D点的俯角α为30°，测得C点的俯角β为60°．则建筑物CD的高度为m（结果不作近似计算）．

查看试题解析
16. 如图，已知四边形ABCD是平行四边形，BC=3AB，A，B两点的坐标分别是（﹣1，0），（0，2），C，D两点在反比例函数y= $\frac{k}{x}$ （x＜0）的图象上，则k的值等于．

查看试题解析

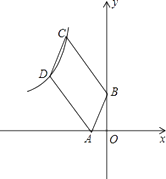
三、计算题

17. 计算：| $\sqrt{3}$ ﹣2|+2010⁰﹣（﹣ $\frac{1}{3}$ ）^﹣¹+3tan30°．

查看试题解析
18. 先化简，后求值： $(\frac{a}{a - 2} - \frac{4}{a^{2} - 2 a}) \div \frac{a + 2}{a^{2}}$ ，其中a=3．

查看试题解析

四、解答题

19. 某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：

(1)、九（1）班的学生人数为，并把条形统计图补充完整；

(2)、扇形统计图中m= ， n= ，表示“足球”的扇形的圆心角是度；

(3)、排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．

查看试题解析
20. 如图，四边形ABCD是边长为a的正方形，点G、E分别是边AB、BC的中点，∠AEF=90°，且EF交正方形外角的平方线CF于点F．

(1)、证明：△AGE≌△ECF；

(2)、求△AEF的面积．

查看试题解析
21. 某商场经营某种品牌的玩具，购进时的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具．

(1)、不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
销售单价（元）
x
销售量y（件）
销售玩具获得利润w（元）

(2)、在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元．

(3)、在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于44元，且商场要完成不少于540件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？

查看试题解析
22. 如图，在矩形ABCD中，点O在对角线AC上，以OA的长为半径的圆O与AD、AC分别交于点E、F，且∠ACB=∠DCE．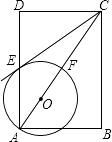

(1)、判断直线CE与⊙O的位置关系，并证明你的结论；

(2)、若tan∠ACB= $\frac{\sqrt{2}}{2}$ ，BC=2，求⊙O的半径．

查看试题解析
23. 如图，已知抛物线经过原点o和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x轴交于点D．直线y=﹣2x﹣1经过抛物线上一点B（﹣2，m）且与y轴交于点C，与抛物线的对称轴交于点F．

(1)、求m的值及该抛物线对应的解析式；

(2)、P（x，y）是抛物线上的一点，若S_△_ADP=S_△_ADC ，求出所有符合条件的点P的坐标；

(3)、点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形．若能，请直接写出点M的运动时间t的值；若不能，请说明理由．

查看试题解析

销售单价（元）	x
销售量y（件）
销售玩具获得利润w（元）