重庆市九龙坡区2018-2019学年中考数学模拟考试试卷

试卷更新日期：2019-06-19 类型：中考模拟

进入出卷网下载

一、选择题：本大题12个小题，每小题4分，共48分。.

1. 清代·袁枚的一首诗《苔》中的诗句：“白日不到处，青春恰自来.苔花如米小，也学牡丹开.”若苔花的花粉直径约为0.0000084米，则数据0.0000084用科学记数法表示为（）

A、8.4×10^-5 B、8.4×10^-6 C、84×10^-7 D、8.4×10⁶

查看试题解析
2. 下列计算正确的是（）

A、2a+3b=5ab B、a²·a⁴=a⁸ C、（-2a²b）³=-8a⁶b³ D、a⁶÷a³+a²=2a²

查看试题解析
3. 如图，AB∥CD，AD=CD，∠1=65°，则∠2的度数是（）

A、50° B、60° C、65° D、70°

查看试题解析
4. 下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 估计（2 $\sqrt{56}$ - $\sqrt{28}$ ）× $\frac{1}{\sqrt{7}}$ 的值应在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
6. 我国古代数学著作《增删算法统宗》记载“绳索量竿”问题：“一条竿子一条索，索比竿子长一托，折回索子去量竿，却比竿子短一托”，其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿子长5尺；如果将绳索对半折后去量竿，就比竿子短5尺。设绳索长为x尺，竿长为y尺，则符合题意的方程组是（）

A、 ${\begin{cases} x = y + 5 \\ 2 x = y - 5 \end{cases}$ B、 ${\begin{cases} x = y - 5 \\ 2 x = y + 5 \end{cases}$ C、 ${\begin{cases} x = y + 5 \\ \frac{1}{2} x = y - 5 \end{cases}$ D、 ${\begin{cases} x = y - 5 \\ \frac{1}{2} x = y + 5 \end{cases}$

查看试题解析
7. 如图，将半径为4，圆心角为90°的扇形BAC绕A点逆时针旋转60°，点B、C的对应点分别为点D、E且点D刚好在上，则阴影部分的面积为（）

A、 $\frac{4 π}{3} + 4 \sqrt{3}$ B、 $\frac{8 π}{3} + 4 \sqrt{3}$ C、 $\frac{4 π}{3} + 2 \sqrt{3}$ D、 $π + 2 \sqrt{3}$

查看试题解析
8. 将一些半径相同的小圆按如图所示的规律摆放，第1个图形有4个小圆，第2个图形有8个小圆，第3个图形有14个小圆，…，依此规律，第9个图形的小圆个数是（）

A、58 B、74 C、92 D、112

查看试题解析
9. 如图所示是一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数y₁= $\frac{k_{1}}{x}$ （x>0）的图象上，顶点B在函数y₂= $\frac{k_{2}}{x}$ （x>0）的图象上，∠ABO=30°，则 $\frac{k_{2}}{k_{1}}$ =（）

A、-3 B、3 C、 $\frac{1}{3}$ D、- $\frac{1}{3}$

查看试题解析
10. 如图，点E是矩形ABCD的边CD上一点，把△ADE沿AE对折，使点D恰好落在BC边上的F点处。已知折痕AE=10 $\sqrt{10}$ ，且CE：CF=4：3，那么该矩形的周长为（）

A、48 B、64 C、92 D、96

查看试题解析
11. 如图，小明利用所学数学知识测量某建筑物BC高度，采用了如下的方法：小明从与某建筑物底端B在同一水平线上的A点出发，先沿斜坡AD行走260米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为72°，建筑物底端B的俯角为63°，其中点A、B、C、D、E在同一平面内，斜坡AD的坡度i=1：2.4，根据小明的测量数据，计算得出建筑物BC的高度约为（）米（计算结果精DE确到0.1米，参考数据：sin72°≈0.95，tan72°≈3.08，sin63°≈0.89，tan63°≈1.96）

A、157.1 B、157.4 C、257.4 D、257.1

查看试题解析
12. 如果关于x的分式方程 $\frac{2 m}{x - 2} + 3 = \frac{x}{2 - x}$ 的解为非负数，且关于x的不等式组 ${\begin{cases} \frac{x - 2 m}{3} \geq 2 \\ x + 4 > 2 (x + 1) \end{cases}$ 无解，则所有符合条件的整数m的个数为（）

A、6 B、5 C、4 D、3

查看试题解析

二、填空题：（本大题6个小题，每小题4分，共24分）

13. 计算： $\sqrt[3]{27}$ - $|- 4|$ +（ $\frac{1}{3}$ ）^-2=.

查看试题解析
14. 已知x-2y=4，xy=4，则代数式5xy-3x+6y的值为.

查看试题解析
15. 如图，已知⊙O的半径为4，OA⊥BC，∠CDA=22.5°，则弦BC的长为.

查看试题解析
16. 经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，这三种可能性大小相同，现有两辆汽车经过这个十字路口，则这两辆汽车都向左转的概率为.

查看试题解析
17. 甲、乙两车分别从A，B两地相向匀速行驶，甲车先出发两小时，甲车到达B地后立即调头，并保持原速度与乙车同向行驶，乙车到达A地后，继续保持原速向远离B的方向行驶，经过一段时间后两车同时到达C地，设两车之间的距离为y（千米），甲车行驶的时间为x小时，y与x之间的函数图象如图所示，则当甲车重返A地时，乙车距离C地千米.

查看试题解析
18. 如图，在边长为6的正方形ABCD中，点E、F、G分别在边AB、AD、CD上，EG与BF交于点I，AE=2，BF=EG，DG>AE，则DI的最小值为.

查看试题解析

三、解答题：（本大题7个小题，每小题10分，共70分）

19. 计算：

(1)、（2a+b）（2a-b）-（2a+b）²+4ab

(2)、 $\frac{4 x^{2} - 12 x}{x^{2} + 8 x + 16} \div \frac{x - 3}{x + 4} + \frac{16}{x + 4}$

查看试题解析
20. 已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：

(1)、∠AEC=∠BED；

(2)、AC=BD．

查看试题解析
21. 中华文明，源远流长，中华汉字，寓意深广。为传承中华优秀传统文化，某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩，学校德育处随机抽取了其中200名学生的成绩作为样本进行统计，制成如下不完整的统计图表：
成绩x（分）分数段
频数（人）
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
0.2
80≤x<90
m
0.35
90≤x<100
50
n
频数分布直方图
根据所给的信息，回答下列问题：

(1)、m=；n=；

(2)、补全频数分布直方图；

(3)、这200名学生成绩的中位数会落在分数段；

(4)、若成绩在90分以上（包括90分）为“优”等，请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人？

查看试题解析

22. 某“兴趣小组”根据学习函数的经验，对函数y=x+

\frac{1}{x}

的图象和性质进行了探究，探究过程如下，请补充完整。

(1)、函数y=x+

\frac{1}{x}

的自变量取值范围是；

(2)、下表是x与y的几组对应值：

…

-3

-2

-1

- $\frac{1}{2}$

- $\frac{1}{4}$

$\frac{1}{4}$

$\frac{1}{2}$

…

- $\frac{10}{3}$

- $\frac{5}{2}$

-2

- $\frac{5}{2}$

- $\frac{17}{4}$

$\frac{17}{4}$

$\frac{5}{2}$

…

则表中m的值为；

(3)、根据表中数据，在如图所示平面直角坐标xOy中描点，并画出函数的一部分，请画出

(4)、观察函数图象：写出该函数的一条性质

(5)、进一步探究发现：函数y=x+

\frac{1}{x}

图象与直线y=-2只有一交点，所以方程x+

\frac{1}{x}

=-2只有1个实数根，若方程x+

\frac{1}{x}

=k（x<0）有两个不相等的实数根，则k的取值范围是。

查看试题解析

23. 每年的3月15日是“国际消费者权益日”，许多家居商城都会利用这个契机进行打折促销活动.甲卖家的A商品成本为600元，在标价1000元的基础上打8折销售.

(1)、现在甲卖家欲继续降价吸引买主，问最多降价多少元，才能使利润率不低于20%？

(2)、据媒体爆料，有一些卖家先提高商品价格后再降价促销，存在欺诈行为.乙卖家也销售A商品，其成本、标价与甲卖家一致，以前每周可售出50件，现乙卖家先将标价提高2m%，再大幅降价24m元，使得A商品在3月15日那一天卖出的数量就比原来一周卖出的数量增加了 $\frac{5}{2}$ m%，这样一天的利润达到了20000元，求m的值.

查看试题解析
24. 如图，在▱ABCD中，CG⊥AB于点G，∠ABF=45°，F在CD上，BF交CG于点E，连接AE，且AE⊥AD.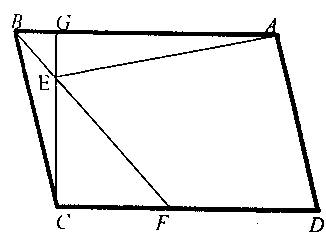

(1)、若BG=2，BC= $\sqrt{29}$ ，求EF的长度；

(2)、求证：CE+ $\sqrt{2}$ BE=AB.

查看试题解析
25. 设a，b是任意两个不等实数，我们规定，满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]。对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”。如函数y=-x+4，当x=l时，y=3；当x=3时，y=1，即当1≤x≤3时，有1≤y≤3所以说函数y=-x+4是闭区间[1，3]上的“闭函数”.

(1)、反比例函数y= $\frac{2019}{x}$ 是闭区间[1，2019]上的“闭函数”吗？请判断并说明理由；

(2)、若二次函数y=x²-6x+k是闭区间[3，4]上的“闭函数”，求k的值；

(3)、若一次函数y=kx+b（k≠0）是闭区间[m，n]上的“闭函数”，求此函数的表达式（可用含m，n的代数式表示）.

查看试题解析

四、解答题：（本大题1个小题，共8分），

26. 如图1，在平面直角坐标系xOy中，二次函数y= $\frac{\sqrt{3}}{2}$ x²- $\sqrt{3}$ x- $\frac{3 \sqrt{3}}{2}$ 的图象与x轴的交点为A，B，顶点为C，点D为点C关于x轴的对称点，过点A作直线l：
y= $\frac{\sqrt{3}}{3}$ x+ $\frac{\sqrt{3}}{3}$ 交BD于点E，连接BC的直线交直线l于K点.

(1)、问：在四边形ABKD内部是否存在点P，使它到四边形ABKD四边的距离都相等？
若存在，请求出点P的坐标；若不存在，请说明理由；

(2)、若M，N分别为直线AD和直线l上的两个动点，连结DN，NM，MK，如图2，求DN+NM+MK和的最小值.

查看试题解析

成绩x（分）分数段	频数（人）	频率
50≤x<60	10	0.05
60≤x<70	30	0.15
70≤x<80	40	0.2
80≤x<90	m	0.35
90≤x<100	50	n