山东省滨州市惠民县2018-2019学年中考数学二模考试试卷
试卷更新日期:2019-06-19 类型:中考模拟
一、选择题:本大题共12个小题,每小题3分,满分36分.
-
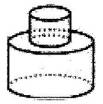
1. 若|-x|=5,则x等于( )A、-5 B、5 C、 D、±52. 已知a=(-3)x(-4),b=(-4)2 , c=(-3)3 , 那么a、b、c的大小关系为( )A、a>b>c B、a>c>b C、c>a>b D、b>a>c3. 将下列图形绕着直线旋转一周正好得到如图所示的图形的是( )
 A、
A、 B、
B、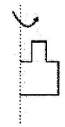 C、
C、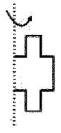 D、
D、 4. 计算正确的是( )A、 B、7a-5a=2 C、(-3a)3=-9a3 D、2a(a-1)=2a2-2a5. 将一副三角板按如图方式摆放,∠1与∠2不一定互补的是( )A、
4. 计算正确的是( )A、 B、7a-5a=2 C、(-3a)3=-9a3 D、2a(a-1)=2a2-2a5. 将一副三角板按如图方式摆放,∠1与∠2不一定互补的是( )A、 B、
B、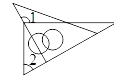 C、
C、 D、
D、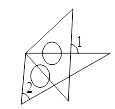 6. 爱心社的志愿者们为品学兼优的家庭困难学生共捐赠资金7000元,已知该资金由25名志愿者捐献,捐献统计情况如下表,则他们捐款金额的中位数和平均数分别是( )
6. 爱心社的志愿者们为品学兼优的家庭困难学生共捐赠资金7000元,已知该资金由25名志愿者捐献,捐献统计情况如下表,则他们捐款金额的中位数和平均数分别是( )金额/元
100
200
300
400
500
人数
2
11
5
4
3
A、200,200 B、200,280 C、300,300 D、300,2807. 某工厂计划生产1500个零件,但是在实际生产时,.…,求实际每天生产零件的个数,在这个题目中,若设实际每天生产零件x个,可得方程 ,则题目中用“……”表示的条件应是( )A、每天比原计划多生产5个,结果延期10天完成 B、每天比原计划多生产5个,结果提前10天完成 C、每天比原计划少生产5个,结果延期10天完成 D、每天比原计划少生产5个,结果提前10天完成8. 如图是在边长为acm的大正方形内放入三个边长都为bcm(a>b)的小正方形纸片,这三张纸片没有盖住的面积是4cm2,则a2-2ab+b2的值为( ) A、2 B、4 C、6 D、89. 已知, 是二元一次方程组 的解,则m+3n的值是( )A、4 B、6 C、7 D、810. 如图,将一张三角形纸片ABC折叠,使点A落在BC边上,折痕EF∥BC,得到△EFG;再继续将纸片沿△BEG的对称轴EM折叠,依照上述做法,再将△CFG折叠,最终得到矩形EMNF,若△ABC中,BC和AG的长分别为4和6,则矩形EMNF的面积为( )
A、2 B、4 C、6 D、89. 已知, 是二元一次方程组 的解,则m+3n的值是( )A、4 B、6 C、7 D、810. 如图,将一张三角形纸片ABC折叠,使点A落在BC边上,折痕EF∥BC,得到△EFG;再继续将纸片沿△BEG的对称轴EM折叠,依照上述做法,再将△CFG折叠,最终得到矩形EMNF,若△ABC中,BC和AG的长分别为4和6,则矩形EMNF的面积为( ) A、5 B、6 C、9 D、1211. 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )
A、5 B、6 C、9 D、1211. 某品牌的饮水机接通电源就进入自动程序:开机加热到水温100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系,直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,水温从100℃降到35℃所用的时间是( )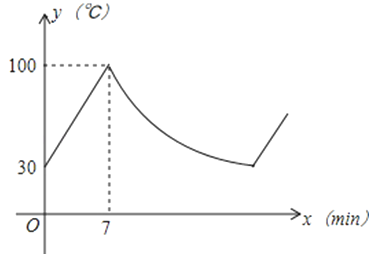 A、27分钟 B、20分钟 C、13分钟 D、7分钟12. 如图,一条抛物线与x轴相交于M、N两点(点M在点N的左侧),其顶点P在线段AB上移动.若点A、B的坐标分别为(一2,3)、(1,3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )
A、27分钟 B、20分钟 C、13分钟 D、7分钟12. 如图,一条抛物线与x轴相交于M、N两点(点M在点N的左侧),其顶点P在线段AB上移动.若点A、B的坐标分别为(一2,3)、(1,3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )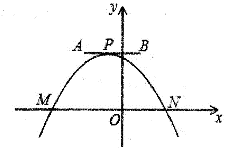 A、-1 B、-3 C、-5 D、-7
A、-1 B、-3 C、-5 D、-7二、填空题:本大题共8个小题,每小题5分,满分40分。
-
13. 计算:(-1)2019-( -2)0=.14. 若一个多边形的每个内角都相等,且都为160°,则这个多边形的内角和是°.15. 某商店老板销售一种商品,他要以不低于进价20%的利润才能出售,但为了获得更多的利润,他以高出进价80%的价格标价,若你想买下标价为360元的这种商品,商店老板让价的最大限度为元16. 除夕晚上小聪和爸爸、妈妈一起玩微信抢红包游戏,他们约定由爸爸在家人微信群中先后发两次“拼手气红包”,每次发放的红包数是3个,每个红包抽到的金额随机(每两个红包的金额都不相等),每次谁抽到红包的金额最大谁就是“手气最佳”者,则两次游戏中小聪都能获得“手气最佳”的概率是。17. 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N使△AMN周长最小,则∠AMN+∠ANM=°.
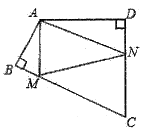 18. 如图,利用四边形的不稳定性改变矩形ABCD的形状,得到▱A1BCD1 , 若▱A1BCD1的面积是矩形ABCD面积的一半,则∠ABA1的度数是.
18. 如图,利用四边形的不稳定性改变矩形ABCD的形状,得到▱A1BCD1 , 若▱A1BCD1的面积是矩形ABCD面积的一半,则∠ABA1的度数是.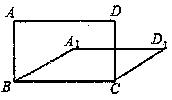 19. 如图,⊙O的直径AB=8,P为O0上任一点(不同于A、B两点),∠APB的平分线交⊙O于点C,弦EF经过AC、BC的中点M、N,则弦EF的长为.
19. 如图,⊙O的直径AB=8,P为O0上任一点(不同于A、B两点),∠APB的平分线交⊙O于点C,弦EF经过AC、BC的中点M、N,则弦EF的长为.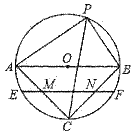 20. 如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1),
20. 如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为(1,1), 是以点B为圆心,BA为半径的圆弧,
是以点B为圆心,BA为半径的圆弧, 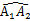 是以点O为圆心,OA1为半径的圆弧,
是以点O为圆心,OA1为半径的圆弧, 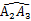 是以点C为圆心,CA2为半径的圆弧,
是以点C为圆心,CA2为半径的圆弧, 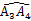 是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5...称为正方形的“渐开线”,那么点A2019的坐标是.
是以点A为圆心,AA3为半径的圆弧,继续以点B、O、C、A为圆心按上述作法得到的曲线AA1A2A3A4A5...称为正方形的“渐开线”,那么点A2019的坐标是. 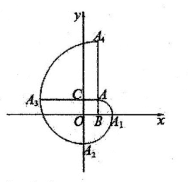
三、解答题:本大题共6个小题,满分74分.
-
21. 设A=(1)、化简A;(2)、当a=3时,记此时A的值为f(3);当a=4时,记此时A的值为f(4);.….解关于x的方程 =f(4)+f(5).22. 在学习因式分解时,我们学习了提公因式法和公式法(平方差公式和完全平方公式),事实上,除了这两种方法外,还有其它方法可以用来因式分解,比如配方法.例如,如果要因式分解x2+2x-3时,显然既无法用提公因式法,也无法用公式法,怎么办呢?
这时,我们可以采用下面的办法:
x2+2x-3=x2+2×x×1+12-1-3 ------------①
=(x+1)2-22 -------------②
解决下列问题:
(1)、填空:在上述材料中,运用了转化的思想方法,使步骤①可以运用公式进行因式分解,这种方法就是配方法;
(2)、显然所给材料中因式分解并未结束,请依照材料因式分解:x2+2x-3(3)、请用上述方法因式分解:4x2-4x-3.23. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交线段BC,AC于点D,E,过点D作DF⊥AC,垂足为F,线段FD,AB的延长线相交于点G.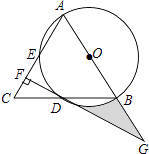 (1)、求证:DF是⊙O的切线;
(1)、求证:DF是⊙O的切线;
(2)、若CF=2,DF=2 ,求图中阴影部分的面积.
24. 如图,直线l:y=kx+6与x轴、y轴分别交于点B、C两点,点B的坐标是(-8,0),点A的坐标为(-6,0). (1)、求k的值.(2)、若点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3?并求出此时直线AP的解析式.
(1)、求k的值.(2)、若点P是直线l在第二象限内一个动点,当点P运动到什么位置时,△PAC的面积为3?并求出此时直线AP的解析式.
(3)、在x轴上是否存在一点M,使得△BCM为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.25. 【模型建立】(1)、如图,△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.
求证:△BEC≌△CDA;
(2)、在平面直角坐标系内将点P(3,2)绕坐标原点逆时针旋转90°,得到点P,求点P'的坐标;(3)、已知一次函数y=2x-4的图象为直线l,将直线l绕它与x轴的交点P逆时针旋转90°,得到直线,求直线l'对应的一次函数解析式。26. 如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上. (1)、求抛物线的解析式;(2)、在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?
(1)、求抛物线的解析式;(2)、在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)、若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标.