河北省保定市唐县2018-2019学年中考数学二模考试试卷
试卷更新日期:2019-06-19 类型:中考模拟
一、选择题(本大题有16个小题,共42分.1~10小题各3分,11~16小题各2分.)
-
1. 早春时节天气变化无常,某日正午气温-3℃,傍晚气温2℃,则下列说法正确的是( )A、气温上升了5℃ B、气温上升了1℃ C、气温上升了2℃ D、气温下降了1℃2. 下列各对数中,数值相等的是( )A、+32与+23 B、-23与(-2)3 C、-32与(-3)2 D、3×22与(3×2)23. 下列四个图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、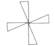 D、
D、 4. 已知三个数-π,-3,-2 ,它们的大小关系是( )A、- π<-2 <-3 B、-3<-π<-2 C、-2 <-π<-3 D、- π<-3<-25. 如图是由棱长为1的几个正方体组成的几何体的三视图,则这个几何体的体积是( )
4. 已知三个数-π,-3,-2 ,它们的大小关系是( )A、- π<-2 <-3 B、-3<-π<-2 C、-2 <-π<-3 D、- π<-3<-25. 如图是由棱长为1的几个正方体组成的几何体的三视图,则这个几何体的体积是( )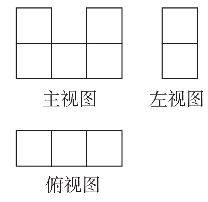 A、3 B、4 C、5 D、66. 如图,数轴上表示 的数对应的点为A点,若点B为在数轴上到点A的距离为1个单位长度的点,则点B所表示的数是( )
A、3 B、4 C、5 D、66. 如图,数轴上表示 的数对应的点为A点,若点B为在数轴上到点A的距离为1个单位长度的点,则点B所表示的数是( ) A、 -1 B、 +1 C、1- 或1+ D、 -1或 +17. 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.从C村到D村的公路平行于从A村到B村的公路,则C,D两村与B,C两村公路之间夹角的度数为( )
A、 -1 B、 +1 C、1- 或1+ D、 -1或 +17. 如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.从C村到D村的公路平行于从A村到B村的公路,则C,D两村与B,C两村公路之间夹角的度数为( ) A、100° B、80° C、75° D、50°8. 化简 的结果是( )A、1 B、 C、 D、09. 甲、乙两支同样的温度计按如图所示的位置放置,如果向左平移甲温度计,使其度数30正对着乙温度计的度数-20,那么此时甲温度计的度数-15正对着乙温度计的度数是( )
A、100° B、80° C、75° D、50°8. 化简 的结果是( )A、1 B、 C、 D、09. 甲、乙两支同样的温度计按如图所示的位置放置,如果向左平移甲温度计,使其度数30正对着乙温度计的度数-20,那么此时甲温度计的度数-15正对着乙温度计的度数是( ) A、5 B、15 C、25 D、3010. 某市公园的东、西、南、北方向上各有一个入口,周末佳佳和琪琪随机从一个入山进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )A、 B、 C、 D、11. 三个全等三角形按下图的形式摆放,则∠1+∠2+∠3的度数是( )
A、5 B、15 C、25 D、3010. 某市公园的东、西、南、北方向上各有一个入口,周末佳佳和琪琪随机从一个入山进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )A、 B、 C、 D、11. 三个全等三角形按下图的形式摆放,则∠1+∠2+∠3的度数是( ) A、90° B、120° C、135° D、180°12. 已知关于x的一元二次方程(k-1)x2+2x+1=0没有实数解,则k的取值范围是( )A、k>2 B、k<2且k≠1 C、k≥2 D、k≤2且k≠113. 对于二次函数y=ax2+4x-1(a≠0)所具有的性质,下列描述正确的是( )
A、90° B、120° C、135° D、180°12. 已知关于x的一元二次方程(k-1)x2+2x+1=0没有实数解,则k的取值范围是( )A、k>2 B、k<2且k≠1 C、k≥2 D、k≤2且k≠113. 对于二次函数y=ax2+4x-1(a≠0)所具有的性质,下列描述正确的是( )
A、图象与x轴的交点坐标是(-1,0) B、对称轴是直线x= C、图象经过点( , ) D、在对称轴的左侧y随x的增大而增大14. 如图,PA,PB分别与半径为3的OO相切于点A,B,直线CD分别交PA,PB于点C,D,并切OO于点E,当PO=5时,△PCD的周长为( ) A、4 B、5 C、8 D、1015. 超市有A,B两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,日无剩油);当日促销活动:购买A型瓶3个或以上,一次性返还现金5元.设购买A型瓶x(个),所需总费用为y(元),则下列说法不一定成立的是( )
A、4 B、5 C、8 D、1015. 超市有A,B两种型号的瓶子,其容量和价格如表,小张买瓶子用来分装15升油(瓶子都装满,日无剩油);当日促销活动:购买A型瓶3个或以上,一次性返还现金5元.设购买A型瓶x(个),所需总费用为y(元),则下列说法不一定成立的是( )型号
A
B
单个瓶子容量(升)
2
3
单价(元)
5
6
A、购买B型瓶的个数是(5 - x)为正整数时的值 B、购买A型瓶最多为6个 C、y与x之间的函数关系式为y=x+30 D、小张买瓶了的最少费用是28元16. 如图,把菱形ABCID向右平移至DCEF的位置,作EG⊥AB,垂足为G,EG与CD相交于点K,GD的延长线交EF于点H,连接DE.则下列结论:
①DG=DE; ②∠DHE= ∠BAD;
③EF+FH=2KC; ④∠B=∠EDH.
则其中所有成立的结论是( )
A、①②③④ B、①②④ C、②③④ D、①③二、填空题(本大题有3个小题,共10分.17~18小题各3分,19小题有2个空,每空2分,)
-
17. 分解因式:xy2-2xy+x=.18. 定义运算a × b,当a≥b时,有a × b=a;当a<b时,有a × b=6.如果(x+2) × 2x=x+2,那么x的取值范围是。19. 如图,正方形ABCD的边长为2,连接BD,点P是线段AD延长线上的一个动点,∠PBQ=45°,点Q是BQ与线段CID延长线的交点,当BD平分∠PBQ时,PD QD(填“>”“<”或“=”);当BD不平分∠PBQ时,PD·QD=。

三、解答题(本大题有7个小题,共68分.)
-
20. 已知y=-1是方程, 的解。(1)、求a的值;(2)、求关于x的不等式1-2(a-1)x<5-a的解集,并将解集在下图所示的数轴上表示出来.
 21. 为了弘扬巾华优秀传统文化,某中学开展了一次“古诗词”知识竞赛.赛程共分“预赛、复赛和决赛”三个阶段,预赛由各班举行,全员参加,按统一标准评分.统计成绩后绘制成图-1和图-2所示的两幅不完整“预赛成绩条形统计图”和“预赛成绩扇形统计图”,预赛前10名选于参加复赛,成绩见“前10名选于成绩统计表”。(采用百分制记分,得分都为60分以上的整数)
21. 为了弘扬巾华优秀传统文化,某中学开展了一次“古诗词”知识竞赛.赛程共分“预赛、复赛和决赛”三个阶段,预赛由各班举行,全员参加,按统一标准评分.统计成绩后绘制成图-1和图-2所示的两幅不完整“预赛成绩条形统计图”和“预赛成绩扇形统计图”,预赛前10名选于参加复赛,成绩见“前10名选于成绩统计表”。(采用百分制记分,得分都为60分以上的整数)
图1 图2
前10名选手成绩统计表
序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
预赛成绩(分)
100
92
95
98
94
100
93
96
95
96
复赛成绩(分)
90
80
85
90
80
88
85
90
86
89
总成绩(分)
94
84.8
89
m
85.6
92.8
88.2
n
89.6
91.8
(1)、求该中学学生的总人数,并将图10-1补充完整;(2)、在图10-2中,求“90.5~100.5分数段人数”圆心角的度数;(3)、预赛前10名选手参加复赛,成绩见“前10名选手成绩统计表”.若按预赛成绩占40%,复赛成绩占60%的比例计算总成绩,并从中选出3人参加决赛,你认为选哪几号选手参加决赛,说明理由.22. 如图,PC是OO的弦,作OB⊥PC于点E,交⊙O于点B,延长OB到点A,连接AC,OP,使∠A=∠P. (1)、求证:AC是⊙O的切线;(2)、若BE=2,PC=4 ,求AC的长.23. 如图,已知反比例函数y= (x>0)的图象与直线l:y=kx+b都经过点P(2,m),Q(n,4),且直线l交x轴于点A,交y轴于点B,连接OP,OQ.
(1)、求证:AC是⊙O的切线;(2)、若BE=2,PC=4 ,求AC的长.23. 如图,已知反比例函数y= (x>0)的图象与直线l:y=kx+b都经过点P(2,m),Q(n,4),且直线l交x轴于点A,交y轴于点B,连接OP,OQ. (1)、直接写出m,n的值及直线l的函数表达式;(2)、△OAP与△OBQ的面积相等吗?写出你的判断,并说明理由;(3)、若点M是y轴上一点,当MP+MQ的值最小时,求点M的坐标.24. 如图1,在等边△ABC和等边△ADP中,AB=2,点P在△ABC的高CE上(点P与点C不重合),点D在点P的左侧,连接BD,ED.
(1)、直接写出m,n的值及直线l的函数表达式;(2)、△OAP与△OBQ的面积相等吗?写出你的判断,并说明理由;(3)、若点M是y轴上一点,当MP+MQ的值最小时,求点M的坐标.24. 如图1,在等边△ABC和等边△ADP中,AB=2,点P在△ABC的高CE上(点P与点C不重合),点D在点P的左侧,连接BD,ED.
图-1 图-2
(1)、求证:BD=CP;(2)、当点P与点E重合时,延长CE交BD于点F,请你在图-2中作出图形,并求出BF的长;(3)、直接写出线段DE长度的最小值.25. 某生产商存有1200千克A产品,生产成本为150元/千克,售价为400元/千克.因市场变化,准备低价一次性处理掉部分存货,所得货款全部用来生产B产品,B产品售价为200元/千.经市场调研发现,A产品存货的处理价格y(元/千)与处理数量x(千克)满足一次函数关系(0<x≤1000),且得到表中数据。x(千克)
y(元/千克)
200
350
400
300
(1)、请求出处理价格y(元/千克)与处理数量x(千克)之间的函数关系式;(2)、若B产品生产成本为100元/千克,A产品处理数量为多少千克时,生产B产品数量最多,最多是多少?(3)、由于改进技术,B产品的生产成本降低到了a元/千克.设全部产品全部售出,所得总利润为W(元).若500<x≤1000时,满足W随x的增大而减小,求a的取值范围.26. 如图,在菱形ABCD中,AB=6,∠ABC=120°,动点P从点B出发,沿BC-CD边以每秒1个单位长度的速度运动,到点D时停止.连接AP,点Q与点B关于直线AP对称,连接AQ,PQ.设运动时间为t(秒).

备用图
(1)、菱形ABCD对角线AC的长为;(2)、当点Q恰在AC上时,求t的值;(3)、当CP=3时,求△APQ的周长;(4)、直接写出在整个运动过程中,点Q运动的路径长.