山东省滨州市邹平县2018-2019学年中考数学模拟考试试卷
试卷更新日期:2019-06-19 类型:中考模拟
一、选择题:
-
1. sin45°的值等于( )
A、 B、 C、 D、2. 在 , , , , , ,这6个数中,无理数共有( )A、4个 B、3个 C、2个 D、1个3. 下列命题中,真命题是( )A、对角线垂直相等的四边形是正方形 B、三角形的一个外角大于它的内角 C、垂直于同一直线的两条直线平行 D、同弧所对的圆周角的度数等于圆心角度数的一半4. 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )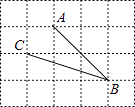 A、2 B、 C、 D、5. 不等式组 的解集在数轴上可以表示为( )A、
A、2 B、 C、 D、5. 不等式组 的解集在数轴上可以表示为( )A、 B、
B、 C、
C、 D、
D、 6. 分式方程 -1= 的解为( )A、 B、 C、无解 D、7. 一元二次方程x2+mx+1=0有实数根,不等式组 有解,则m应满足的条件是( )A、 B、 C、 或 D、8. 如图所示,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B,E是半圆弧的三等分点,弧BE的长为 ,则图中阴影部分的面积为( )
6. 分式方程 -1= 的解为( )A、 B、 C、无解 D、7. 一元二次方程x2+mx+1=0有实数根,不等式组 有解,则m应满足的条件是( )A、 B、 C、 或 D、8. 如图所示,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E.B,E是半圆弧的三等分点,弧BE的长为 ,则图中阴影部分的面积为( ) A、 B、 C、 D、9. 已知直线y=(m-3)x-3m+1不经过第一象限,则m的取值范围是( )A、 B、 C、 D、10. 已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A、 B、 C、1或 D、1或11. 如图,正方形ABCO的边长为4,点E在线段AB上运动,AE=BF,且AF与OE相交于点P,直线y= x-3与x轴、y轴交于M、N两点,连接PN,PM,则△PMN面积的最大值( ).
A、 B、 C、 D、9. 已知直线y=(m-3)x-3m+1不经过第一象限,则m的取值范围是( )A、 B、 C、 D、10. 已知点平面内不同的两点A(a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为( )A、 B、 C、1或 D、1或11. 如图,正方形ABCO的边长为4,点E在线段AB上运动,AE=BF,且AF与OE相交于点P,直线y= x-3与x轴、y轴交于M、N两点,连接PN,PM,则△PMN面积的最大值( ). A、 B、12 C、 D、1512. 如图,在ΔABC中, , ,作 的内切圆 ,分别与 、 、 相切于点 、 、 ,设 ,ΔABC的面积为 ,则 关于 的函数图象大致为( )
A、 B、12 C、 D、1512. 如图,在ΔABC中, , ,作 的内切圆 ,分别与 、 、 相切于点 、 、 ,设 ,ΔABC的面积为 ,则 关于 的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每题5分,满分40分,将答案填在答题纸上)
-
13. 在平面直角坐标系中,已知一次函数y=-3x+1的图象经过A(x1 , y1)、B(x2 , y2)两点,若x1>x2 , 则y1y2(用“>”或“<”填空).14. 函数 中,自变量x的取值范围是 .15. 有一组数据如下:3,a , 4,6,7,它们的平均数是5,那么这组数据的方差。16. 在△ABC中,∠C=90°,sinA= ,BC=4,则AB值是 .17.
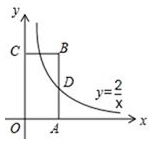
如图,反比例函数 的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为.
 18. 从数-2,- ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn,则正比例函数y=kx的图象经过第三、第一象限的概率是 .19.
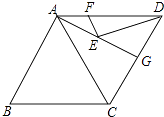
18. 从数-2,- ,0,4中任取一个数记为m,再从余下的三个数中,任取一个数记为n,若k=mn,则正比例函数y=kx的图象经过第三、第一象限的概率是 .19.如图,在菱形ABCD中,AB=6,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是 .
 20. 观察下列关于自然数的等式:
20. 观察下列关于自然数的等式:①
②
③
根据上述规律解决下列问题:
猜想第 个等式(用含 的式子表示).
三、解答题 (本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)
-
21. 先化简,再求值:(x-1)÷( -1),其中x为方程x2+3x+2=0的根.22. 为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:

(Ⅰ)被抽样调查的学生有人,并补全条形统计图;
(Ⅱ)每天户外活动时间的中位数是(小时);
(Ⅲ)该校共有2000名学生,请估计该校每天户外活动时间超过1小时的学生有多少人 ?
23. 如图,⊙O是△ABC的外接圆,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于点E,交PC于点F,连接AF. (1)、求证:AF是⊙O的切线;(2)、若AB=8,tanB= ,求线段CF、PC的长.24. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 ,已知点O与球网的水平距离为5m,球网的高度为1.55m.
(1)、求证:AF是⊙O的切线;(2)、若AB=8,tanB= ,求线段CF、PC的长.24. 甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式 ,已知点O与球网的水平距离为5m,球网的高度为1.55m. (1)、当a=- 时,①求h的值;②通过计算判断此球能否过网.(2)、若甲发球过网后,羽毛球飞行到与点O的水平距离为7m , 离地面的高度为 m的Q处时,乙扣球成功,求a的值.25. 如图,一次函数y1=kx+b的图象与反比例函数y2= 的图象交于点A、B两点,与x轴、y轴交于C、D两点,且点C、D刚好是线段AB的三等分点,OD=2,tan∠DCO=
(1)、当a=- 时,①求h的值;②通过计算判断此球能否过网.(2)、若甲发球过网后,羽毛球飞行到与点O的水平距离为7m , 离地面的高度为 m的Q处时,乙扣球成功,求a的值.25. 如图,一次函数y1=kx+b的图象与反比例函数y2= 的图象交于点A、B两点,与x轴、y轴交于C、D两点,且点C、D刚好是线段AB的三等分点,OD=2,tan∠DCO= (1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积;(3)、若y1≤y2 , 请直接写出相应自变量x的取值范围26. 如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M , 设点P的横坐标为t .
(1)、求一次函数与反比例函数的解析式;(2)、求△AOB的面积;(3)、若y1≤y2 , 请直接写出相应自变量x的取值范围26. 如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M , 设点P的横坐标为t .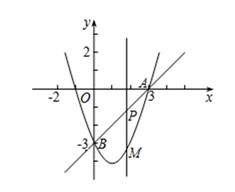 (1)、分别求出直线AB和这条抛物线的解析式.(2)、若点P在第四象限,连接AM、BM , 当线段PM最长时,求△ABM的面积.(3)、是否存在这样的点P , 使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
(1)、分别求出直线AB和这条抛物线的解析式.(2)、若点P在第四象限,连接AM、BM , 当线段PM最长时,求△ABM的面积.(3)、是否存在这样的点P , 使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.