2016-2017学年广西贵港市港南区八年级下学期期中数学试卷
试卷更新日期:2017-05-31 类型:期中考试
一、选择题
-
1. 正方形的面积是4,则它的对角线长是( )A、2 B、 C、2 D、42. 平行四边形、矩形、菱形、正方形都具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直平分且相等3. 在下列以线段a、b、c的长为边,能构成直角三角形的是( )A、a=3,b=4,c=6 B、a=5,b=6,c=7 C、a=6,b=8,c=9 D、a=7,b=24,c=254. 若四边形的两条对角线相等,则顺次连接该四边形各边中点所得的四边形是( )A、梯形 B、矩形 C、菱形 D、正方形5. 如果梯子的底端离建筑物5米,13米长的梯子可以达到建筑物的高度是( )A、12米 B、13米 C、14米 D、15米6. 一个多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是( )A、6条 B、7条 C、8条 D、9条7. 直角三角形斜边上的中线长是6.5,一条直角边是5,则另一直角边长等于( )A、13 B、12 C、10 D、58. 一直角三角形的两边长分别为3和4.则第三边的长为( )A、5 B、 C、 D、5或9.
如图,一棵树在一次强台风中,从离地面5 m处折断,倒下的部分与地面成30°角,如图所示,这棵树在折断前的高度是( )
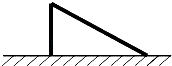 A、10m B、15m C、5m D、20m10. 如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是14,则DM等于( )
A、10m B、15m C、5m D、20m10. 如图,在▱ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,▱ABCD的周长是14,则DM等于( ) A、1 B、2 C、3 D、411. 如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )
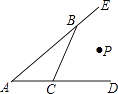
A、1 B、2 C、3 D、411. 如图,AC,BD是平行四边形ABCD的对角线,AC与BD交于点O,若AC=4,BD=5,BC=3,则△BOC的周长是( )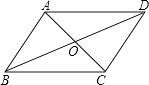 A、7.5 B、6 C、12 D、1012. 如图,已知点P到AE、AD、BC的距离相等,下列说法:
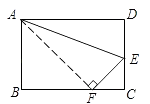
A、7.5 B、6 C、12 D、1012. 如图,已知点P到AE、AD、BC的距离相等,下列说法:①点P在∠BAC的平分线上;
②点P在∠CBE的平分线上;
③点P在∠BCD的平分线上;
④点P在∠BAC,∠CBE,∠BCD的平分线的交点上.
其中正确的是( )
 A、①②③④ B、①②③ C、④ D、②③
A、①②③④ B、①②③ C、④ D、②③二、填空题
-
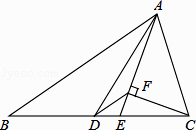
13. 若直角三角形的一个锐角为50°,则另一个锐角的度数是 度.14. 已知菱形的两条对角线的长分别为5和6,则它的面积是 .15. 平行四边形的周长为24cm,相邻两边长的比为3:1,那么这个平行四边形较短的边长为 cm.16. 如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为 .
 17. 如图,平行四边形ABCD中,AB=AD=6,∠DAB=60度,F为AC上一点,E为AB中点,则EF+BF的最小值为 .
17. 如图,平行四边形ABCD中,AB=AD=6,∠DAB=60度,F为AC上一点,E为AB中点,则EF+BF的最小值为 .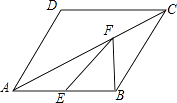 18. 如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为 .
18. 如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为 .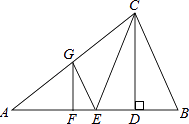
三、解答题
-
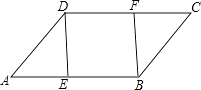
19. 如图,在▱ABCD中,E、F分别是AB、DC边上的点,且AE=CF.
求证:△ADE≌△CBF.
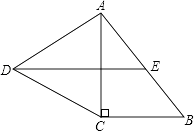
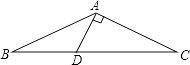
 20. 如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,
20. 如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:BC=3AD.
 21. 如图、四边形ABCD中,AB=AD=6,∠A=60°,∠ADC=150°,已知四边形的周长为30,求四边形ABCD的面积.
21. 如图、四边形ABCD中,AB=AD=6,∠A=60°,∠ADC=150°,已知四边形的周长为30,求四边形ABCD的面积.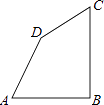 22. 若三角形的三个内角的比是1:2:3,最短边长为1,最长边长为2.求:(1)、这个三角形各内角的度数;(2)、另外一条边长的平方.23. 如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
22. 若三角形的三个内角的比是1:2:3,最短边长为1,最长边长为2.求:(1)、这个三角形各内角的度数;(2)、另外一条边长的平方.23. 如图,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.求证:
 (1)、PE=PF;(2)、点P在∠BAC的角平分线上.
(1)、PE=PF;(2)、点P在∠BAC的角平分线上.