广东省深圳市宝安区2017届九年级下学期第二次调研数学试题
试卷更新日期:2017-05-31 类型:中考模拟
一、选择题
-
1. -5的倒数是( )A、5 B、-5 C、 D、2. 国务院总理李克强在《2017年国务院政府工作报告》中提到,2016年新增第四代移动通信用户3.4亿,数据“3.4亿”用科学记数法表示为( )A、3.4×106 B、3.4×108 C、34× 107 D、3.4×1093. 下列各图中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、2a2·a3=2a6 B、(3ab)2=6a2b2 C、2abc÷ab=2 D、3a2b+ba2=4a2b5.
4. 下列运算正确的是( )A、2a2·a3=2a6 B、(3ab)2=6a2b2 C、2abc÷ab=2 D、3a2b+ba2=4a2b5.如图,直线AB//CD,点E是BC上一点,连接AE,若∠DCB=35°,∠EAB=23°,则∠AEC的度数是( )
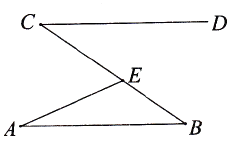 A、58° B、45° C、23° D、60°6. 深圳市统计局发布的2016年《深圳市气候数据每日观测记录》显示,2016年12月26—21日这六天的平均相对湿度(百分数)分别是58,50,45,54,64,82.对于这组数据,以下说法正确的是( )A、平均数是59 B、中位数是56 C、众数是82 D、方差是377. 中国CBA篮球常规赛比赛中,每场比赛都要分出胜负,每队胜1场得 2分,负1场得1分.今年某队在全部38场比赛中得到70分那么这个队今年胜的场次是( )A、6场 B、31场 C、32场 D、35场8. 定义一种新运算:a♣b=a(a-b),例如,4♣3=4(4-3)=4.若x♣2=3,则x的值是( )A、x=3 B、x=-1 C、x1=3,x2=1 D、x1=3,x2=-19. 若方程mx+ny=6的两个解是 , ,则m,n的值为( )A、 B、 C、 D、10.
A、58° B、45° C、23° D、60°6. 深圳市统计局发布的2016年《深圳市气候数据每日观测记录》显示,2016年12月26—21日这六天的平均相对湿度(百分数)分别是58,50,45,54,64,82.对于这组数据,以下说法正确的是( )A、平均数是59 B、中位数是56 C、众数是82 D、方差是377. 中国CBA篮球常规赛比赛中,每场比赛都要分出胜负,每队胜1场得 2分,负1场得1分.今年某队在全部38场比赛中得到70分那么这个队今年胜的场次是( )A、6场 B、31场 C、32场 D、35场8. 定义一种新运算:a♣b=a(a-b),例如,4♣3=4(4-3)=4.若x♣2=3,则x的值是( )A、x=3 B、x=-1 C、x1=3,x2=1 D、x1=3,x2=-19. 若方程mx+ny=6的两个解是 , ,则m,n的值为( )A、 B、 C、 D、10.如何求tan75°的值?按下列方法作图可解决问题.如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD.连接此图可求得tan75°的值为( )
 A、2- B、2+ C、1+ D、 -111.
A、2- B、2+ C、1+ D、 -111.如图点O是△ABC外接圆的圆心,连接OB,若∠1=37°,则∠2的度数是( )
 A、52° B、51° C、53° D、50°12.
A、52° B、51° C、53° D、50°12.如图,直线l分别交x轴、y轴于点A、B,交曲线y= (x>0)于点C,若AB:AC=1:3,且S△AOB= ,则k的值为( )
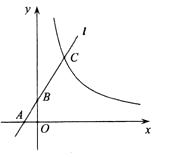 A、 B、2 C、 D、
A、 B、2 C、 D、二、填空题
-
13. 因式分解:m3-2m2+m=.14. 在一个口袋中有4个完全相同的小球,把它们分别标号为①,②,③,④,随机地摸出一个小球,记录后放回,再随机摸出一个小球,则两次摸出的小球的标号相同的概率是.15.
如图所示,每一个图形都是由形状相同的五角星按一定规律组成的,其中第①个图形中一共有9个五角星,第②个图形中一共有17个五角星,第③个图形中一共有25个五角星,……,按此规律排列,则第n个图形中五角星的个数为.
 16.
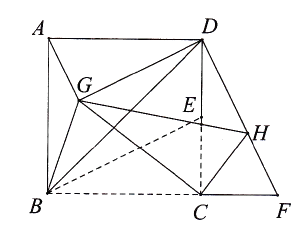
16.如图,在边长为2 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.
三、解答题
-
17. 计算:18. 先化简分式: ,再从不等式组 的解集中选出合适的整数作为a的值,代入求值.19.
深圳市教育局在全市中小学开展“四点半活动”试点工作.某校为了了解学生参与“四点半活动”项目的情况,对初中的部分学生进行了随机调查,调查项目分为“科技创新”类、“体育活动”类、“艺术表演”类、“植物种植”类及“其它”类共五大类别,并根据调查的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题

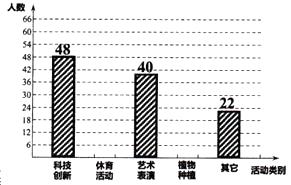 (1)、请求出此次被调查学生的总人数人.(2)、根据以上信息,补全频数分布直方图.(3)、求出扇形统计图中,“体育活动”α的圆心角等于度.(4)、如果本校初中部有1800名学生,请估计参与“艺术表演”类项目的学生大约多
(1)、请求出此次被调查学生的总人数人.(2)、根据以上信息,补全频数分布直方图.(3)、求出扇形统计图中,“体育活动”α的圆心角等于度.(4)、如果本校初中部有1800名学生,请估计参与“艺术表演”类项目的学生大约多少人?
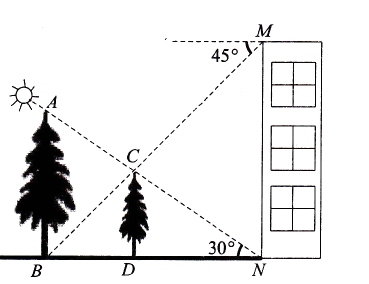
20.如图,在楼房MN前有两棵树与楼房在同一直线上,且垂直于地面,为了测量树AB,CD的高度,小明爬到楼房顶部M处,光线恰好可以经过树CD的顶部C点到达树AB的底部B点,俯角为45°,此时小亮测得太阳光线恰好经过树CD的顶部C点到达楼房的底部N点,与地面的夹角为30°,树CD的影长DN为15米.请求出树AB、CD的高度?(结果保留根号)
 21. 某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表去年销售总额为80000元,今年A型智能手表的售价每只比去年降低了600元,若售出的数量与去年相同,销售总额将比去年减少了25%.(1)、请问今年A型智能手表每只售价多少元?(2)、今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价格与销售价格如表.若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?
21. 某科技公司研发出一款多型号的智能手表,一家代理商出售该公司的A型智能手表去年销售总额为80000元,今年A型智能手表的售价每只比去年降低了600元,若售出的数量与去年相同,销售总额将比去年减少了25%.(1)、请问今年A型智能手表每只售价多少元?(2)、今年这家代理商准备新进一批A型智能手表和B型智能手表共100只,它们的进货价格与销售价格如表.若B型智能手表进货量不超过A型智能手表数量的3倍,所进智能手表可全部售完,请你设计出进货方案,使这批智能手表获利最多,并求出最大利润是多少元?A型智能手表
B型智能手表
进价
1300元/只
1500元/只
售价
今年的售价
2300元/只
22.如图1,在平面直角坐标系xOy中,点A( ,0),B(3 ,0),以AB为直径的⊙G交y轴于C,D两点.
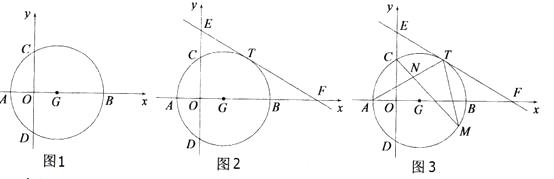 (1)、填空:请直接写出⊙G的半径r,圆心G的坐标:r=;G( , ).(2)、如图2,直线y= 与x、y轴分别交于F、E两点,且经过圆上一点T( ,m),求证:直线EF是⊙G的切线;(3)、在(2)的条件下,如图3,点M是⊙G优弧 上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.23.
(1)、填空:请直接写出⊙G的半径r,圆心G的坐标:r=;G( , ).(2)、如图2,直线y= 与x、y轴分别交于F、E两点,且经过圆上一点T( ,m),求证:直线EF是⊙G的切线;(3)、在(2)的条件下,如图3,点M是⊙G优弧 上的一个动点(不包括A、T两点),连接AT、CM、TM,CM交AT于点N,试问,是否存在一个常数k,始终满足CN·CM=k?如果存在,请求出k的值,如果不存在,请说明理由.23.如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,且OC=3OA,点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.
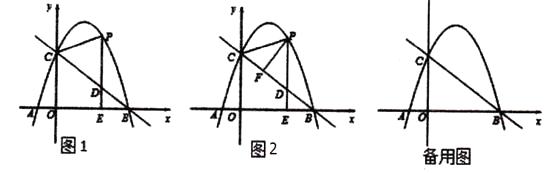 (1)、试求抛物线的解析式;(2)、如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.(3)、当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由.
(1)、试求抛物线的解析式;(2)、如图2,当动点P只在第一象限的抛物线上运动时,过点P作PF⊥BC于点F,试问△PFD的周长是否有最大值?如果有,请求出最大值;如果没有,请说明理由.(3)、当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四 边形CDPQ能否成为菱形?如果能,请求此时点P的坐标;如果不能,请说明理由.