2016年广东省深圳市17校联考中考数学二模试卷
试卷更新日期:2017-05-31 类型:中考模拟
一、选择题
-
1. 给出四个数0, ,π,﹣1,其中最小的是( )A、0 B、 C、π D、﹣12. 据深圳特区报3月30日早间消息,华为公司获得2016中国质量领域最高奖.华为公司将2016年销售收入目标定为818亿美元,是国内互联网巨头BAT三家2014年收入的两倍以上.其中818亿美元可用科学记数法表示为( )美元.A、8.18×109 B、8.18×1010 C、8.18×1011 D、0.818×10113. 在奔驰、宝马、丰田、三菱等汽车标志图形中,为中心对称图形的是( )
A、 B、
B、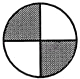 C、
C、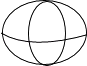 D、
D、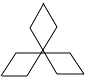 4. 马大哈做题很快,但经常不仔细思考,所以往往错误率很高,有一次做了四个题,但只做对了一个,他做对的是( )A、a8÷a4=a2 B、a3•a4=a12 C、 =±2 D、2x3•x2=2x55. 下列各图中,描述∠1与∠2互为余角关系最准确的是( )A、
4. 马大哈做题很快,但经常不仔细思考,所以往往错误率很高,有一次做了四个题,但只做对了一个,他做对的是( )A、a8÷a4=a2 B、a3•a4=a12 C、 =±2 D、2x3•x2=2x55. 下列各图中,描述∠1与∠2互为余角关系最准确的是( )A、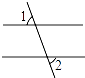 B、
B、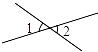 C、
C、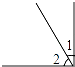 D、
D、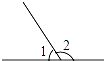 6. 如图,正三棱柱的主视图为( )
6. 如图,正三棱柱的主视图为( )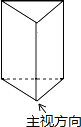 A、
A、 B、
B、 C、
C、 D、
D、 7. 2015赛季中超联赛中,广州恒大足球队在联赛30场比赛中除4月3日输给河南建业外,其它场次全部保持不败,取得了67个积分的骄人成绩,已知胜一场得3分,平一场得1分,负一场得0分,设广州恒大一共胜了x场,则可列方程为( )A、3x+(29﹣x)=67 B、x+3(29﹣x)=67 C、3 x+(30﹣x)=67 D、x+3(30﹣x)=678. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= AC•BD,其中正确的结论有( )
7. 2015赛季中超联赛中,广州恒大足球队在联赛30场比赛中除4月3日输给河南建业外,其它场次全部保持不败,取得了67个积分的骄人成绩,已知胜一场得3分,平一场得1分,负一场得0分,设广州恒大一共胜了x场,则可列方程为( )A、3x+(29﹣x)=67 B、x+3(29﹣x)=67 C、3 x+(30﹣x)=67 D、x+3(30﹣x)=678. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= AC•BD,其中正确的结论有( )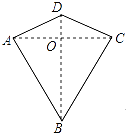 A、0个 B、1个 C、2个 D、3个9. 深圳空气质量优良指数排名近年来一直排在全国城市前十.下表是深圳市气象局于2016年3月22日在全市十一个监测点监测到空气质量指数(AQI)数据如表
A、0个 B、1个 C、2个 D、3个9. 深圳空气质量优良指数排名近年来一直排在全国城市前十.下表是深圳市气象局于2016年3月22日在全市十一个监测点监测到空气质量指数(AQI)数据如表监测点
荔园
西乡
华侨城
南油
盐田
龙岗
洪湖
南澳
葵涌
梅沙
观澜
AQI
15
31
25
24
31
24
25
25
34
20
26
质量
优
优
优
优
优
优
优
优
优
优
优
上述(AQI)数据中,众数和中位数分别是( )
A、25,25 B、31,25 C、25,24 D、31,2410. 如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于 BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( )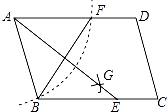 A、11 B、6 C、8 D、1011. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )
A、11 B、6 C、8 D、1011. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x= ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③a﹣b+c=0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2 . 上述说法正确的是( )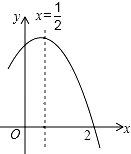 A、①②③④ B、③④ C、①③④ D、①②12. 如图,两个反比例函数y1= (其中k1>0)和y2= 在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )
A、①②③④ B、③④ C、①③④ D、①②12. 如图,两个反比例函数y1= (其中k1>0)和y2= 在第一象限内的图象依次是C1和C2 , 点P在C1上.矩形PCOD交C2于A、B两点,OA的延长线交C1于点E,EF⊥x轴于F点,且图中四边形BOAP的面积为6,则EF:AC为( )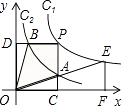 A、 ﹕1 B、2﹕ C、2﹕1 D、29﹕14
A、 ﹕1 B、2﹕ C、2﹕1 D、29﹕14二、填空题
-
13. 已知a≠0,a≠b,x=1是方程ax2+bx﹣10=0的一个解,则 的值是 .14. 周星驰拍摄的电影《美人鱼》取景地在深圳杨梅坑,据称是深圳最美的溪谷,为估计全罗湖区8000名九年级学生云过杨梅坑的人数,随机抽取400名九年级学生,发现其中有50名学生去过该景点,由此估计全区九年级学生中有个学生去过该景点.15.
将一些相同的“○”按如图所示的规律依次摆放,观察每个“稻草人”中的“○”的个数,则第20个“稻草人”中有个“○”.
 16. 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC= ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .
16. 如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC= ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为 .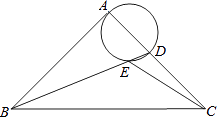
三、解答题
-
17. 计算:|﹣ |+(2016﹣π)0﹣2sin45°+( )﹣2 .18. 解不等式组 .并写出它的整数解.19. 九年级(1)班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有10人,请解答下列问题:
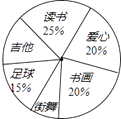 (1)、该班的学生共有名;该班参加“爱心社”的人数为名,若该班参加“吉他社”与“街舞社”的人数相同,则“吉他社”对应扇形的圆心角的度数为;(2)、一班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.20. 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
(1)、该班的学生共有名;该班参加“爱心社”的人数为名,若该班参加“吉他社”与“街舞社”的人数相同,则“吉他社”对应扇形的圆心角的度数为;(2)、一班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.20. 如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.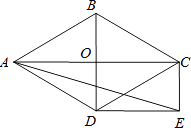 (1)、求证:四边形ODEC是矩形;(2)、当∠ADB=60°,AD=2 时,求sin∠AED的值.21. 如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20 米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】
(1)、求证:四边形ODEC是矩形;(2)、当∠ADB=60°,AD=2 时,求sin∠AED的值.21. 如图,河坝横断面背水坡AB的坡角是45°,背水坡AB长度为20 米,现在为加固堤坝,将斜坡AB改成坡度为1:2的斜坡AD【备注:AC⊥CB】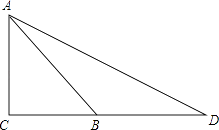 (1)、求加固部分即△ABD的横截面的面积;(2)、若该堤坝的长度为100米,某工程队承包了这一加固的土石方工程,为抢在在汛期到来之际提前完成这一工程,现在每天完成的土方比原计划增加25%,这样实际比原计划提前10天完成了,求原计划每天完成的土方.【提示土石方=横截面x堤坝长度】22. 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
(1)、求加固部分即△ABD的横截面的面积;(2)、若该堤坝的长度为100米,某工程队承包了这一加固的土石方工程,为抢在在汛期到来之际提前完成这一工程,现在每天完成的土方比原计划增加25%,这样实际比原计划提前10天完成了,求原计划每天完成的土方.【提示土石方=横截面x堤坝长度】22. 如图,点O为Rt△ABC斜边AB上一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.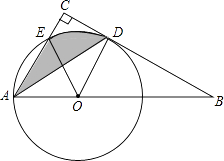 (1)、求证:AD平分∠BAC;(2)、若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).23. 如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B(3,0).
(1)、求证:AD平分∠BAC;(2)、若∠BAC=60°,OA=2,求阴影部分的面积(结果保留π).23. 如图,抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)、B(3,0). (1)、求b、c的值;(2)、如图1直线y=kx+1(k>0)与抛物线第一象限的部分交于D点,交y轴于F点,交线段BC于E点.求 的最大值;(3)、如图2,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.问在直线BC下方的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求b、c的值;(2)、如图1直线y=kx+1(k>0)与抛物线第一象限的部分交于D点,交y轴于F点,交线段BC于E点.求 的最大值;(3)、如图2,抛物线的对称轴与抛物线交于点P、与直线BC相交于点M,连接PB.问在直线BC下方的抛物线上是否存在点Q,使得△QMB与△PMB的面积相等?若存在,求出点Q的坐标;若不存在,请说明理由.